|
| Next section | Beginning of notes | End of section | Index of notes | Syllabus | Announcements |
| Last revised 1999/01/17 |
|
| Next section | Beginning of notes | End of section | Index of notes | Syllabus | Announcements |
| Last revised 1999/01/17 |
Since so many good ideas fail in practice, there are degrees of confidence that scientists have in current explanations. Lots of additional data must be gathered before you can be confident that a given good idea is indeed a correct idea. In fact, individual scientists can easily become so attached to their beautiful ideas that they fail to give them up even though the weight of evidence is against them. Sometimes this reluctance turns into a good thing, for experiments can be wrong or misleading or both, and theories that had been given up for dead are sometimes resurrected. Scientific progress is made by various people making the best possible cases for conflicting ideas, until the evidence is so strong that even the strongest partisans of losing ideas give up or simply die off. Not that you can determine the likelihood of a theory being correct by counting noses. Some people show themselves more capable of judging what works and what does not, and their opinions count more than the opinions of less skillful scientists. What happens is that as more and more evidence comes in, the community reaches a consensus and attention passes to other questions. Those people who are too inflexible to change their minds are left behind.
There are a set of words applied to scientific explanations that reflect the degree of confidence that the community has in the explanation. Since the passage from relative lack of confidence to relatively high confidence is a fuzzy process, the terminology is fuzzy also. Oversimplifying a bit, explanations which we would be startled to find to be incorrect are called laws. Sets of explanations taken together are called theories. Unfortunately "theory" is also sometimes used to refer to a set of descriptions that fit together but haven't yet been adequately tested. A guess about what objects and process may be present in a system is sometimes called a model. There is a "Standard Model" of particle physics, naming the particles and the forces they exert, and this model is generally believed to be quite reliable. Unfortunately for standard terminology, the word model is also used for a theory that amounts to a metaphor. You may feel that one system acts somewhat like another system which you already understand, but isn't just an example of the one you understand. In this case you refer to your hypothesis that the two systems act similarly as being a "model" of the new system. A model may eventually become a theory, especially if the mathematics of the new system is shown to be the same as the mathematics of the old one even though the systems are not identical.
Not all sensible questions can be investigated at any given time, nor are all answerable questions recognized when they first become tractable. For any given problem, you must have enough data to allow you to see the patterns. If the technology to permit you to get the data does not yet exist, you have no chance of understanding the problem. Moreover, one of the most important clues as to whether an idea is or is not likely to be right is how well the explanation fits with the patterns seen in similar phenomena, especially phenomena that are more easily investigated. If the corresponding areas of science have not yet been investigated, it may be very difficult to decide whether you really understand the problem you are working on. Also, many times no one realizes that a particular set of phenomena might be understandable, or simpler than it appears, or have some other reason to be interesting. In that case, no one works on that problem. The one way to be absolutely sure that no one will understand a phenomenon is for no one to work on it.
In the physical sciences, "simple patterns" usually translates to "mathematics." Physics in particular has been built up by a process of generating pictures that explain things, converting the pictures to mathematical statements, and then learning to treat the mathematics as a set of pictures to be borrowed to understand the next-most-difficult concepts. Then the advanced understanding is written down mathematically, that mathematics is converted into a set of visualizations, and the whole process repeated, over and over. The method is very powerful, but it yields a physics where the real meaning is mathematics that may take a long time to understand, and the English explanations are merely translations of the mathematics. The English is less reliable than the mathematics because it cannot incorporate all the nuances of the mathematics. Still, there is a lot of meaning available from the English without using all of the mathematics. The problem is that when the mathematics is modified a little bit, the English sometimes has to be modified a lot. The continuity of the developing set of explanations then is not apparent unless you spend more time learning mathematics than makes sense for a non-specialist in the field.
In this course we will for the most part use English descriptions. I will expect that, if given the proper information, you will be able to interpret an algebraic statement, but I will not expect you to be able to manipulate algebraic expressions. The result is much like studying French literature in English translation; the basic meaning is accessible but the nuances are not. I have felt that I have gained from learning about French literature without being able to read the original French very well. I hope to make it possible for you to understand what is going on in part of science and why it is interesting without having to dig through the mathematics. If you want the nuances, you will need to do further work after the course is finished. Another analogy: this course is like one which shows you great paintings and helps you enjoy them; it does not try to teach you how to paint. It will, however, try very hard to help you understand what the painting process is like.
As I first wrote this there was an ad in the Physics Commons Room that started out "Astrophysics is supposed to make you feel clueless...." [I won't mention the product.] On it one of our astrophysicists had written "After all, it makes astrophysicists feel clueless." This course should provide a few clues for cosmology and particle physics. It won't provide all of them because nobody has found all of them and probably no one ever will. If you like to solve puzzles, think of a situation where you can solve parts of the puzzle, but you never finish the whole thing. The puzzle just gets bigger. "If you see light at the end of the tunnel, build more tunnel." [W. B. Daniels, quoted way out of context.]
The way you find the simple processes underlying complicated data is to find patterns in the data. Finding patterns involves organizing the data in many different ways until you see a regularity. One of the things we will do in this course is to look for these regularities in particle data that I will give you. Of course we must somehow figure how to look for the patterns. To show the process in a simpler situation, next time I will take data from Nuclear Physics which has patterns that are somewhat like those in Particle Physics and show how to go about finding the patterns. The patterns in Particle Physics are different and richer than those in Nuclear Physics, but you can see from the analysis of nuclei many or most of the techniques you need to analyze particles.
Special Relativity and Quantum Mechanics are consistent with each other, but General Relativity and Quantum Mechanics are not. Presumably there is something still to be understood by studying phenomena in which gravity and Quantum Mechanics both matter.
The universe could be finite or infinite in space. If it were infinite in space, you could travel forever in at least one direction without ever coming back to the region you started from. Either way, finite or infinite, there is a bit of a philosophical puzzle. Infinite space is a bit difficult to visualize, to say the least. On the other hand, if the universe has a boundary and you go to the edge, what do you see on the other side of the boundary? This question is easy to answer mathematically but the answer is not so easy to understand. We need something familiar to think about in the hopes of being able to apply at least part of what we know about the simple "model" in understanding how the universe could be finite. Specifically, it is helpful to consider the surface of the Earth as a model for a possible appearance of a finite Universe. The area of the earth is finite, about 13.6 million square miles, but it does not have any "edge." You can go as far as you like along the surface. You will never find a boundary, but after a while you will be again be travelling in the same area where you started out. The Universe could be the same way. If you could travel far enough, you might simply come back where you started and retrace your original path. The Universe would be finite, but with no boundary enclosing it.
In the case of the Earth, the surface is two-dimensional and curves into a third dimension. It is fairly easy to visualize what is going on. In the case of a finite Universe with no boundary, there could not be an additional dimension for space to curve into. The Universe is everything that exists. If an extra dimension existed it would be part of "everything that exists" and therefore part of the Universe. The three dimensions must in some sense curve into each other. It is possible to describe mathematically a space that curves in such a way as to be finite, have no boundary, and imply no extra dimensions, but visualizing such a space is another matter altogether. The Universe, finite or infinite, is curved in that manner. Given what we know at the moment, it is most likely that the Universe is curved in such a way as to be infinite in extent. However, the question of the finiteness of the Universe is still open.
There is a similar problem with a Universe that begins or ends at some given time. If "everything there is" started at some set time, what was present before that time? If it ends, what will there be after it is gone? One might imagine using the same solution as for a spatially-finite universe: at some point you come back to the beginning and start over again. There has been some thought along those lines, but as far as I know no one seriously advocates a universe which is exactly the same after some set time interval. Such a situation would in any event violate Quantum Mechanics, which we have much reason to believe. The more common solution to the finiteness problem is to say that time is a property of the universe itself so that it simply doesn't make sense to ask about what was before or what will come after. I am tempted to call that the "cop-out" technique, but it isn't clear that there is a better solution.
In any event the Universe we live in seems to have had a beginning and may or may not have an ending. In fact, the laws of physics require the Universe to have either a beginning time or an ending time and also require that the density of the Universe at that time be infinite. The reason is that the Law of Gravity precludes a stable, static Universe with no beginning or ending. All massive bodies attract each other by exerting gravitational forces. If you try to fill the Universe with objects in random directions these attractive forces pull all the objects closer and closer together. The objects simply won't stay in their own spots. This problem was noted already in Newton's time, and various efforts were made to cure it. Newton himself argued, incorrectly, that in an infinite universe no object would know which direction to move and so the Universe would be stable. However, at best all the objects in such a Universe would get closer and closer together in such a way that the process looked exactly the same wherever you were. If in fact any point in the Universe were to have a slightly higher density than the rest, no matter how slight, all nearby masses would eventually collect around that point. A static Universe could not exist.
You can avoid having everything fall into one "Big Crunch" by having all the masses moving away from each other from the beginning. Then gravity will slow them down but not necessarily turn them around. You have no Big Crunch at the end of time. However, if you look back at where the masses came from, they had to be once much closer together if they are now getting further apart. So there must have been a time when they were all very close together but moving apart. This isn't a Big Crunch, but it does look like a big explosion and is generally referred to as a "Big Bang." Newtonian gravity seems not to be consistent with a Universe that has been and will be here forever. There must be either a beginning or an end.
Einstein's General Relativity shares the "flaw" of Newton's Theory of Gravity in that it does not permit a static universe. Einstein was so unhappy about this situation that he arbitrarily inserted a term, the "Cosmological Constant," into his equations to allow the Universe to be static and stable. When it was discovered observationally that the universe was expanding, he gladly dropped the term.
Now observational data seems to require that we put the Cosmological Constant back in. We will discuss why in fifteenth section of the notes.
So much for theory. What is the Universe really like?
As we saw in the video Powers of Ten, stars are grouped into galaxies and galaxies are grouped into clusters. There is even some evidence that, further out than the video went, the clusters are themselves clustered. I cannot show you directly what our own galaxy looks like. Since we are inside the galaxy, our pictures do not show the structure. Instead, the picture shows the Whirlpool Galaxy and its smaller companion. [Hubble image from a web page by William C Keel at the University of Alabama]. The larger galaxy is of the same type as our own, a spiral. The small glob at the upper left is a companion elliptical galaxy. Elliptical galaxies have an overall elliptical shape and do not have spiral arms. A third type of galaxy, called irregular, neither has spiral arms nor a clean elliptical shape. Our galaxy has two small irregular galaxies, called the Large Magellanic Cloud and the Small Magellanic Cloud, as companions. Unfortunately, neither of them can be seen from the northern hemisphere.


The Hubble Space Telescope has taken a picture in a "typical" region of the sky which shows one of the most distant known clusters. Since light takes time to get to us from such long distances, this cluster is also among the youngest known. The Space Telescope Science Institute provided the picture. [All STScI digital images are available royalty-free, provided proper attribution is given. The conditions of use are given on their web site. The remainder of this paragraph is a paraphrase of their caption for this photograph.] The leftmost picture shows the area of the sky where the cluster was photographed. The small square in that picture shows the location that was photographed to get the middle picture. The middle picture contains the cluster itself, and the really little square in the middle picture is the region that is enlarged in the picture on the upper right. That picture shows one of the galaxies. The distant galaxy is not the bright object but rather the small blob on the right-hand side. There are fourteen other galaxies in the middle picture that are at similar distances. The faintest objects in the middle picture are all at a very large distance from the earth, but most of the brighter ones are relatively nearby galaxies.

Hubble can take advantage of the fact that galaxies that are a long way away must be younger. Here we have a series of pictures from Hubble showing galaxies at different distance and hence of different ages. The caption from the Space Telescope Science Institute explains what is shown. At the top left is a contemporary elliptical galaxy, and at the lower left a contemporary spiral. These are labelled (at the top) with an estimate of the age of the universe, 14 billion years. The second column from the left shows three galaxies when the universe was only 9 billion years old. The top galaxy is elliptical, the other two are spirals. The two right-hand columns show corresponding galaxies at times of 5 billion years and of 2 billion years. (Neither the age of the universe nor the time when galaxies first appeared are known to high accuracy).

In conclusion,
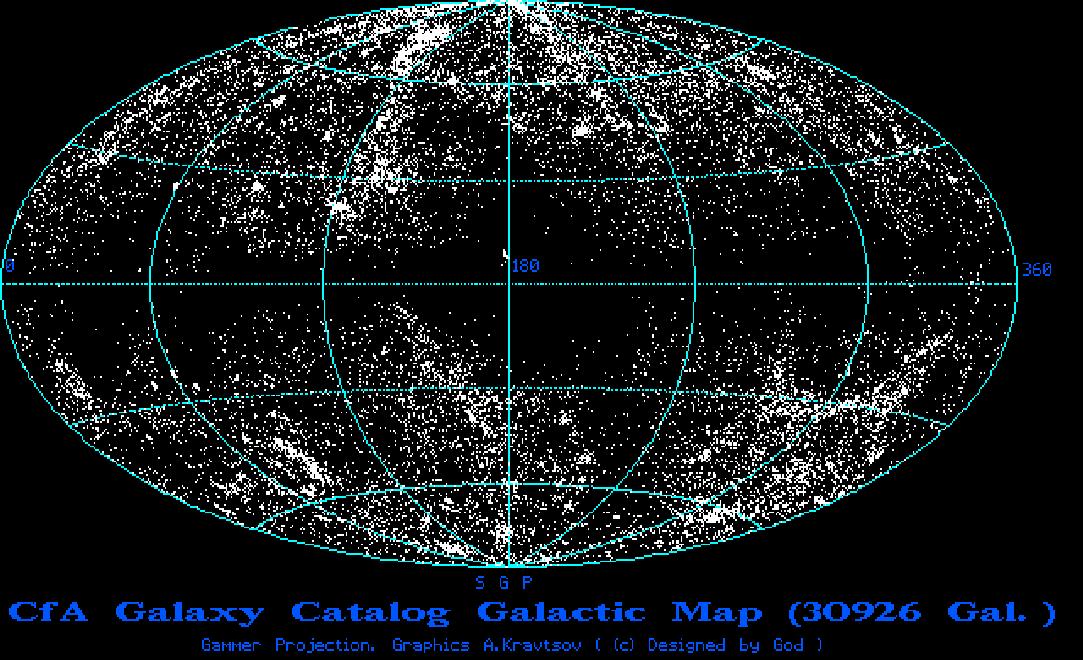
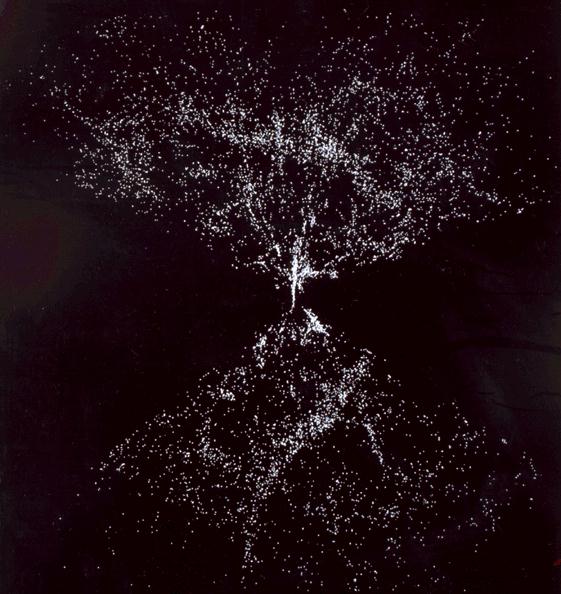
This picture shows the distribution along one band in the sky at all distances. The angle in the sky is given by the angle in the picture (duh!) and the distance of the point from the center of the picture gives the distance of the galaxy from us. The dark bands to either side are caused by the dust clouds, again. The tendancy to have fewer points far from the center is because the galaxies gradually get too faint to see. Again, the distribution is well described as a uniform distribution of small clumps. You probably see some patterns in the distribution of clumps. Since, unlike with Rorschach ink blots or the "canals" of Mars, different people generally see the same patterns, the patterns are probably real.
| Next section | Beginning of notes | Top | Index of notes | Syllabus | Announcements |