Quarks, Gluons, and the Big Bang

1. Aristotle vs. Galileo
2. Newton's Laws
   1. Newton's Laws of Motion
   2. Newton's Law of Gravity
   3. Implications
      1. Nonexistence of absolute rest and absolute position
      2. Absolute time

1. Roemer's measurement of speed of light
2. Maxwell's theory of fixed speed of light
3. Interpretation of Maxwell's theory as involving the ether
4. Michelson and Morely's experimental refutation of the ether

1. Postulates
   1. All laws of physics are the same and independent of the velocity of the observer
   2. The speed of light is the same for all observers, independent of their velocities
2. Consequences
   1. Mass and Energy:
      E = m c², where E is the energy; m is the mass; c [speed of light] is the highest possible speed
   2. There is no absolute time
3. Space-time coordinates
4. The light-cone [difficult section]

1. Inconsistency of Newton's Gravity with Special Relativity, because of instantaneous propagation
2. Gravity as warping of space-time
3. Geodesics: straight lines in space-time do not seem straight in 3-d space
4. Consequences
   1. Bending of light, seen at eclipses
   2. Time slows near masses, directly measured
   3. Space-time is dynamic, not static

1. General introduction
2. Fixed speed of light
3. Coordinate transformations
4. Length contraction
5. Time dilation
6. Paradoxes to think about
   1. Muon lifetime
   2. Train in tunnel

1. Energy, mass, and velocity
2. That pesky (+-) sign
3. The speed limit
4. Tachyons
5. The light cone
6. Absence of absolute time [details if there is time]

1. Muon lifetime
2. Train in tunnel

Special Relativity is probably the most misunderstood theory of physics. Fewer people know anything about General Relativity or Quantum Mechanics, but for no other theory in physics have so many people been told so many things about the theory that are philosophically important and wrong. It is widely agreed that Einstein taught us that "all things are relative" and "nothing is absolute." Neither of these are any part of Special Relativity, which simply gives transformation rules that allow one person to translate his measurements so that they will agree with the measurements of other, moving, people. We need some of these transformation rules for particle physics, especially the rules about energies, and we might as well learn a little about the conceptual aspects of special relativity while we are at it.

Special Relativity does have some strange aspects, all well tested experimentally. There is a speed limit; nothing moving at a speed less than the speed of light can ever move move faster than light. Moving objects contract, really contract, not just appear to contract. In a lecture or two we will show how to temporarily "put a four-car train in a two-car tunnel" with closed doors at each end of the tunnel. Time slows down at high velocities as well, and we will talk about a concrete example of that as well. Although Einstein denied using the experiment in constructing the theory, logically these phenomena all follow from a difficult experiment done in a scientifically obscure country a decade before the end of the 19th century....

In 1887, Albert Michelson and Albert Morely, working at the Case School of Applied Science in Cleveland, Ohio, performed a clever little experiment that showed that the speed of light measured by any observer is independent of the speed of the source of the light and also independent of the speed of the observer. Light is different than sound, the other travelling wave that we know well. Sound moves through air and travels at a set rate relative to the air. Hence if you move while making a sound, the speed of the sound wave as you measure it is different than it was when you were stationary. Similarly the speed of a sound you detect depends on how you are moving through the air carrying the sound. In contrast, the speed of light does not depend on the speed of source or observer, and there is no medium "carrying" the light. The Michelson-Morley experiment was the first experiment done in the US that was of any significance to physics since Benjamin Franklin somehow managed to avoid getting himself killed while investigating lightning.

OK, so what? The problem is that now two observers moving with respect to each other must disagree about how far apart different objects are. Consider a man to be moving very fast past a woman, whom we will call stationary [she is stationary]. Have either of them click a flashlight on and off very quickly when they pass. After a short time we can draw where he is, where she is, and the various places where the light given off by the flashlight is.

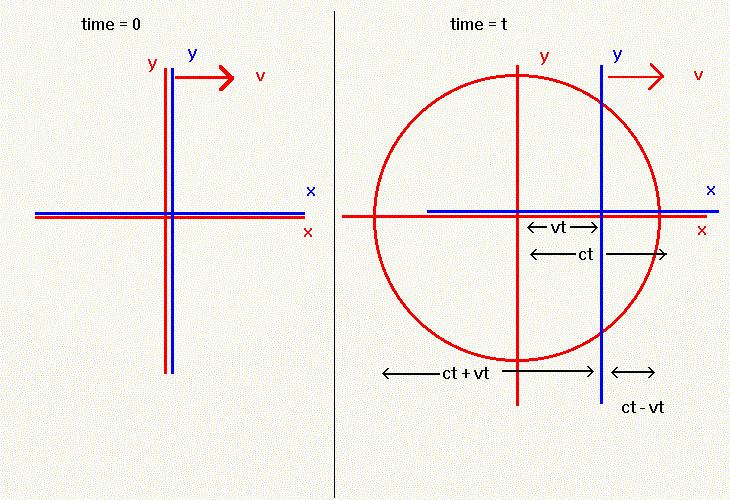
Aside on speeds: If you travel 30 mi/hr for one hour, you go 30 miles. If you travel at the same speed for two hours, you go 30 x 2 = 60 miles. In general, the distance d you will go at a speed v travelling for a time t is d=vt.

You wanted a problem? We've got a problem. Measured distances depend on who you are! How do we escape? There must be a prescription that allows any observer to determine what any other observer will get as a result of a time or distance measurement, with only her measurement of his velocity as a parameter. Further, the laws of physics should have the same form after the translation as before, and each observer's translation law should be the same.

Funny things are going to have to happen here to make it possible to translate the measurements of one observer into the measurements of the other while allowing both to get the same number for the speed of light. Lengths of objects will wind up smaller when measured by the moving observer, and time intervals will be longer. Still, a translation law does exist. The translation can be found using only the diagram in the previous section, and experience shows that it works in all other situations as well. The result is

We are using x to represent [store a value for measurements of] positions and t to represent times. The quantity v represents the "relative" velocity, the velocity of the moving observer as measured by the stationary observer. Finally, c represents the speed of light.

We must be extraordinarily careful about what time and distance measurements we put where in these equations. The combination

is the position and time of an event as measured by the moving observer, and

is the position and time of the same event as measured by the stationary observer. Note that it isn't the event that is moving or stationary, it is the observer. Since different observers do not get the same numbers for the position of the same event, we must always be careful to specify who is doing the measurement. Also notice that neither measurement is the "true" one, but rather both are equally valid.

The "stationary" observer is the one who made the measurement of the velocity v. If the moving observer measures the relative velocity, he gets -v. The -v means that he sees her moving at the same speed as she says he is moving, only in the opposite direction.

Now that we have written down the actual transformations, we can look at two of their more interesting features. First, if you want to interchange the role of the observers, considering the man stationary and the woman moving, then you must change the labels "moving" to "stationary", "stationary" to "moving", "she" to "he" and "he" to "she". To allow for the fact that a different observer is now defining the relative velocity you must also change v to -v everywhere [remember, he got -v and she got v for their relative velocity].

The two equations will have to be solved for x_moving and t_moving , a bit of nuisance that is not fit for people but is properly a job for a computer-algebra program. The result is a pair of equations identical to the originals! This identity says that the specification of which observer is moving and which stationary is arbitrary, so at least the translation-law part of the physics is independent of observer.

The second interesting feature of these transformations is the factor

which looks like it might be no more than an annoying distraction. However, if we graph its size for various values of v, we find that when the velocity becomes nearly c the factor has a large effect:

Relativistic Factor

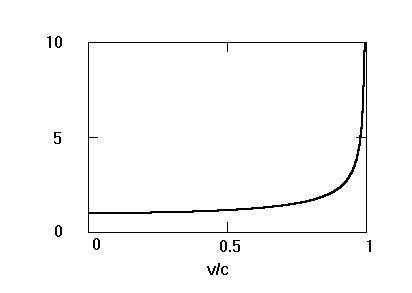
On the other hand, at normal speeds you can't see any effect at all from this factor. At a decent walking speed of 2 miles/hour, which is 3 feet or about 1 meter per second, the relativistic factor is about 1 + 5 x 10^-18 or 1.000,000,000,000,000,005 . Because of the small size of the relativistic factor at small speeds, you cannot see any relativistic effects until velocities get fairly close to the speed of light.

There are actually translation rules for Newtonian physics, as well. The nonrelativistic rules are much simpler than the relativistic ones. We will be able to understand them by walking around the classroom a bit during the lecture. They are

You may have heard people state an answer to the question "What is the length of a moving rod compared to its length at rest?" The answer to this question is simple [it is given below ], but the question itself is not. First, special relativity only tells us relationships between the measurements made by moving observers, and there are no explicit observers in this question. Frequently, in fact, the first thing you must do in science to answer a question is to make it more precise, and we must do exactly that here. Our question really means "What is the length of a rod, moving with respect to a 'stationary' observer and measured by that observer, compared to the length as measured by an observer moving along with the rod?" Next, we must define carefully what we mean by measuring the length of a rod. The definition is easy for the observer moving with the rod but not for the stationary observer:

1. The length of the rod for the moving observer is the distance between the two ends of the rod or in other words the difference between the position of one end of the rod and the position of the other end of the rod. Since the moving observer is not moving relative to the rod, neither of these numbers depends on time.
2. The length of the rod for the stationary observer is the difference between the positions of the two ends of the rod both measured at the same time. If the two positions are not measured at the same time, the movement of the rod will mess up the determination of its length. Nitpicking, right? Not quite. Because of the transformation law for times measured by different observers (given above), the two observers disagree about what "the same time" means for events at different places. When that disagreement is taken into account algebraically, the behavior of the length of the moving rod is given by
   (L for stationary observer) = (L for moving observer) sqrt(1 - v² / c² )

   

   (L for stationary observer) / (L for moving observer)

   which is the opposite of what I would have guessed looking at the equations giving the translation of x between observers. [Compare the graph for changes of time intervals given below.]

   At ordinary speeds this contraction is of no importance whatsoever. At a walking speed of about 1 meter/second, my one-foot-thick body would contract by 5 x 10^-18 foot = 0.000,000,000,000,000,005 foot, an amount which I could accomplish as easily by leaving out of my snacks about one molecule per day of chocolate.

3. Time dilation

   Let's jump straight to the precisely formulated question for time intervals. We are interested, for example, in the length of time between ticks of a particular clock wherever it may be. The precise way to state that question is "What is the time between ticks of a clock, moving with respect to a 'stationary' observer and measured by that observer, compared to the time between ticks as measured by an observer moving along with the clock?" We can then define the time between ticks as

   1. The time between ticks for the moving observer is the difference between the time of the second tick and the time of the first tick at the point where the clock is sitting. Since the moving observer is not moving relative to the clock, both of these positions are the same.
   2. The time between ticks for the stationary observer is the difference between the time of the second tick and the time of the first tick at the point where the clock is sitting. Since the clock is moving with respect to the observer, these two positions are not the same. These definitions are not like the definitions of the measurement of length. The length measurements were to be made at the same time as seen by the observer doing the measurement. The time measurements are not to be made at the same position but rather at the potentially changing position of the clock. When the definitions are pursued algebraically, the result is
      (clock tick for stationary observer) = (clock tick for observer moving with clock) / sqrt(1 - v² / c² )

      

      (clock tick for stationary observer) / (clock tick for moving observer)

      [Compare the graph for lengths given above.]

      The relation between time intervals is the opposite of the relation between the lengths of a rod measured by different observers. The time intervals between ticks of a clock are longer for the observer moving with respect to the clock than they are for an observer moving with the clock (not shorter, as lengths are). The principles of special relativity are easy to state, but the implications of those principles are not easy to anticipate.

      Again, at ordinary speeds time dilation is of no importance whatsoever. If I were to walk at a speed of about 1 meter/second for an hour, my body would age just a bit more slowly due to the relativistic time dilation. As a result, I would live 5 x 10^-18 hour = 0.000,000,000,000,000,005 hour longer, an amount which is swamped by the extra life expectancy gained from the exercise.

   3. Paradoxes
      1. Muon lifetime

         Muons are made at the top of the atmosphere by cosmic rays, and some of them travel toward the surface of the earth at a speed comparable to the speed of light. However, their lifetime as measured in the laboratory is so short that even the speed of light x the muon's lifetime [cT] is smaller than the distance to the ground. Since c is the highest possible speed of the muon and its lifetime is the longest time it can travel, cT should be the furthest the muon can possibly travel. Nonetheless, muons are observed at the surface. How? Once you figure out why, look at the process from the standpoint of the muons.

      2. Train in tunnel

         A train is approaching a tunnel which, when both are at rest, is twice its length. At the speed the train is going its length is just less than 1/2 of its rest length, so for an observer who is stationary with respect to the tunnel the train is just shorter than the tunnel. The tunnel has doors in order to keep snowdrifts off the tracks, and an operator opens the front door in time to let the train in, closes the door after the end of the train goes into the tunnel, and then opens the back door to let the train out. The train, being shorter than the tunnel, can fit between the closed doors. OK?

         The engineer of the train sees the tunnel as being only 50% of its rest length and therefore 75% shorter than the train. How will the train get through???

   Mass, Energy, and the Absolute Speed Limit

   1. Energy, mass, and velocity

      A surprising result from special relativity is that the velocity of light is the largest possible velocity. There is a slight caveat to that statement, which will be much clearer when we see how the rule comes about.

      First we must review the technical meaning of energy. If you have had a chemistry course you have heard most or all of what I have to say, but I may well say it differently to emphasize the aspects of energy that are relevant to relativity. Energy is a quantity that is used to determine as much as you can about the movement of objects without actually solving the equations of motion. Energy can change from one form to another, but if you chase down all the places where it can possibly hide, the total energy in an isolated system never changes. Some possible forms of energy are

      1. Kinetic energy of a body, the energy it has because it is moving. Specifically, for small velocities (compared to the speed of light)
         E = ¹/₂ m v²
         where m is the mass of the object and v is its velocity. The diagram shows how the size of E varies with the velocity.
         

      2. Potential Energy. If you drop an eraser, its velocity gets bigger and bigger, so its kinetic energy is increasing. If its total energy is to be constant, some kind of energy must be decreasing. The kind that is decreasing is its potential energy, the energy it has because of its being in a position where it might be accelerated by a force. There are rules for calculating the potential energy when you know the force and ways to show that the total energy is really constant. We don't really need the rules. We do need to know that this form of energy exists.

      3. Thermal Energy. This form of energy is actually the kinetic energy of the atoms that make up the object.

      4. Chemical Energy. A particular form of potential energy due to the electrical forces among the electrons and protons that make up an atom.

      Friction in this view is simply a way of transferring the kinetic energy of an object into thermal energy, heating up the surfaces that are sliding across each other.

      In special relativity, the kinetic energy is given by a rather different-looking formula:

      E = m c² / [ (+-) sqrt( 1 - v² / c² ) ]

      In this formula there is a square root in the denominator, and mathematically this square root may have either a positive or negative sign, as we indicate with the (+ -) symbol. The ambiguous sign is because

      [-sqrt(a)]² = [+sqrt(a)]² = a

      and any quantity whose square is a is a square root of a. We have no obvious use for the minus sign, since kinetic energies are always positive, so we will ignore it for the moment. [We will find out that this decision is a mistake, but more about that problem later.]

      The graph of the energy as a function of velocity is quite different when the relativistic effects are taken into account:

      

      Notice that for small v, the left-hand part of the graph, the curve looks much like the nonrelativistic form except that the kinetic energy is no longer zero for v = 0. Einstein interpreted this state of affairs as representing a contribution of the mass of the object to the total energy of the system. That contribution is simply the value of the energy at v = 0, which is

      E = (+ -) m c²

      This interpretation, ignoring the technically ambiguous sign, was confirmed by the discovery of nuclear decay and the (kinetic) energy released by the decay.

      The similarity of the relativistic energy near v = 0 to the classical kinetic energy is not an accident. Special Relativity always gives the ordinary, classical result when the velocity is small. Otherwise Relativity would have been discovered much sooner than it was.

   2. That pesky (+ -) sign. Discussed on a separate page.

   3. The speed limit

      Now we can see where the speed limit comes from, and the precise form of the law. To increase the velocity of any object, its kinetic energy must be increased. Since energy overall is constant, some other kind of energy must be decreased by the same amount. Checking the graph of relativistic kinetic energy against velocity, we see that to push the velocity of the object all the way to c, an infinite amount of that other form of energy must be available. Since there is no way to provide an infinite amount of energy, the object cannot be pushed to a speed of c. Similarly, if an object is travelling faster than the speed of light, it will take an infinite amount of energy to get its speed down to the speed of light. So the rule is actually that no object's speed can pass through the speed of light.

   4. Tachyons

      Since the rule says only that an object moving less than the speed of light can never travel at a speed greater than that of light, there is still a possibility that there might be particles that always travel faster than light. These particles have been named tachyons just in case they actually exist. They would be very funny objects indeed. First, their kinetic energy would be smallest at very large velocities and would become zero as their velocity became infinite [look at the equation above]. Second, their kinetic energy would look like

      E = mass (speed of light)2 / sqrt(- a positive number)    = mass (speed of light)2 / [sqrt(-1) sqrt(a positive number)]

      [the positive number is v²/c² - 1]. The sqrt(-1) is not an ordinary number, and in particular the energy of an object cannot involve sqrt(-1). Hence the only way tachyons could exist would be if mass = M sqrt(-1) , so that

      E = [M sqrt(-1) (speed of light)2 / [sqrt(-1) sqrt(a positive number) ]    = M (speed of light)2 / [sqrt(a positive number) ]

      (In the last line we have divided numerator and denominator by sqrt(-1) .)

      In spite of their strangeness, tachyons have been looked for extensively in experiments. None have been found, and it is safe to say that most physicists would be very surprised if one were found. That does not mean that we should stop looking.

   5. The light cone

      Because nothing can travel faster than the speed of light, there is no way that two objects can exchange information in less time than given by the distance between them divided by the speed of light (x/c). Hence if the sun disappeared right now, it would be 8 minutes (the time it takes for light to travel to the earth from the sun) before anything on earth could be affected by the disappearance. We can show pictorially where/when objects may be to affect us or to be affected by us. The border in space/time between objects that can affect each other and those that can't is called the light cone and is shown in Figure 2.7, p. 29, in Hawking. The figure is easier to understand if you watch it being constructed on the blackboard, which I will do at this point.

   6. Absence of absolute time [details in class if there is time]

   Resolution of our Paradoxes

   1. Muon Lifetime
      • Produced near top of atmosphere, very roughly at 10,000 m

      • Lifetime of

                -6
        2.2 x 10   seconds
        

      • Traveling at the speed of light

              8
        3 x 10  m/s
        

        they can travel only 660 m, so how do they reach the ground?

      ---

      From our point of view

      • Energy/mass = 20 (approximately)

      • Hence the relativistic factor is about 20

      • Hence their lifetime is 20 times larger

      • Hence they can go 660 x 20 m = 13,200 m in their lifetime as we measure it, which is far enough.

      ---

      From the muon's point of view

      • The relativistic factor is still 20, but it is applied to the distance to the ground. The lifetime is of course the lifetime as measured by an observer stationary with respect to the muon.

      • Hence the distance to the ground is 20 times shorter

      • The distance to the ground is 10,000m / 20 = 500 m, and the 660 m available to travel is ample.

   2. Train in tunnel

      Point of view of the tunnel operator

      • Four-car train

      • Tunnel with length of two-car train, with doors at each end, only one of which may be open at a time.

      • Train has energy of a bit more than twice its mass

      • The relativistic factor is 2.

      • As measured by the tunnel operator, the train's length is 4 cars/2 = 2 cars; it fits.

      ---

      Point of view of the train's engineer

      • The relativistic factor is still 2

      • As measured by the engineer, the tunnel's length is 2 cars/2 = 1 car-length; the train will not fit inside.

      • Fortunately, what is simultaneous in the tunnel viewpoint does not have to be simultaneous in the train viewpoint, and both doors are open, allowing the train to steam right through.

   Next section

   Previous section

   Beginning of section

   Index of notes

   Syllabus

   Announcements