|
| Next section | Previous section | End of section | Index of notes | Syllabus | Announcements |
|
| Next section | Previous section | End of section | Index of notes | Syllabus | Announcements |
| Last revised 1999/05/04 |
These principles can be understood through analogies. Suppose you see two people who are about to collide with each other. How do you get them to avoid the collision? You would have to call out before the collision to warn them to avoid each other. Of course, you have to call early enough for the sound wave to get to them. If you need a faster signal, you could use light to carry the message. But they can only know something you told them if there has been time to get a message to them. There is no way you could ever have signalled anyone who has always been on the other side of the horizon, because there has never been enough time for any signal to have reached them.
In a Universe with a finite lifetime, you can only have affected the behavior of objects that at some time were no further away than the distance light could have travelled since the Universe began.
Now suppose there were too many people at the back of the room and too few at the front? How could we get everyone spread out evenly? Somehow some people have to move from the back at least partway toward the front. Messages and bodies have to move from one place to the other in order to even out the numbers. None of this can be done at speeds greater than that of light. So, barring some magical effect that makes all densities the same for no reason, two places can have the same mass density only if the matter at each place has had enought time to affect the behavior of the matter at the other. Since they can have affected each others' behaviors only when they were within each others' horizons, two areas can be expected to have the same density only if they were at some time within each others' horizons.
But this restriction causes us a problem. We can see matter in any direction out to distances near the horizon. We can see cosmic background radiation in any direction out essentially to the horizon. Two regions sending background radiation to us from opposite directions are well over a horizon distance apart from each other, in fact essentially two full horizons apart. If space has been expanding without acceleration over the entire lifetime of the Universe, such locations have never been close enough to affect each other. Hence in a nonaccelerating, expanding Universe, you can arrange for all visible parts of the Universe to be at the same density only by magic. So now an entirely different theme comes up: How uniform is the Universe in space and time?
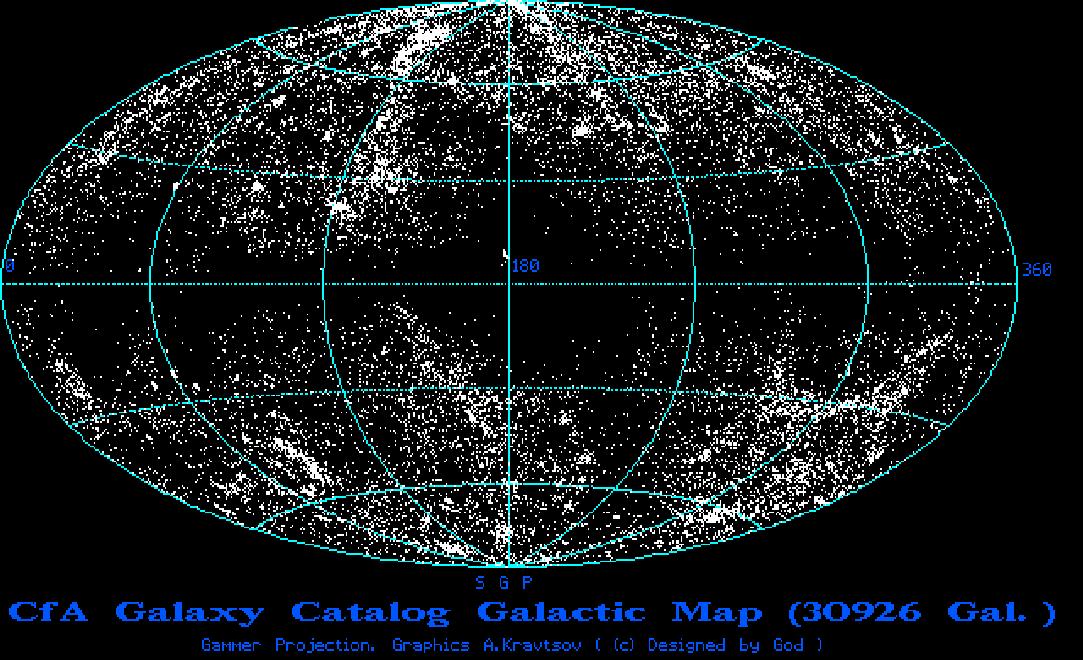
The dark band across the center of the diagram is caused by absorption of light inside our own galaxy, presenting us from seeing all of the other galaxies in those particular directions. Otherwise the distribution is somewhat spotty, but with the same average density in all directions.
We can see the constant density even more clearly in the distribution of galaxies in space. The next picture can be found many places on the web, including a page from National Academy Publications, which publishes documents for the National Academy of Sciences.
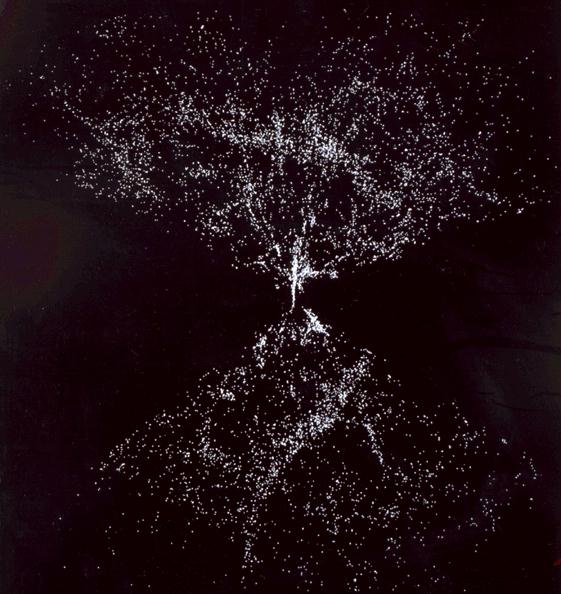
The gap at either side of this distribution is caused by absorption of light within our own galaxy. Within the rest of the distribution you can see clusters, lines of high density which are projections of flat, pancake-like structures, and regions, called "voids," that are virtually empty of galaxies. Nonetheless, on the whole the density is fairly constant when averaged over modest-sized volumes.
The similar appearance of the Universe in various directions is even more obvious in the distribution of the cosmic background radiation shown in the NASA diagram here:

The average temperature of the radiation diagrammed here is 3K, and the variations in temperature are quoted as having a maximum of +-150 x 10 -6 K, so the radiation is constant within an impressive 5 parts per 100,000!
Overall, the data strongly support Friedmann's two postulates (see text, page 40)
The Universe appears to be much more uniform than special relativity allows without arbitrarily set initial conditions.
It seems that we need some magic. The name of the magic is ...
The energy given to space is called the "vacuum energy," and the associated mass is normal in the sense that it produces a curvature to space that is just like that given by a uniform mass distribution. Thus the vacuum energy contributes just like matter in determining whether the Universe is finite or infinite. The associated mass is abnormal, however, in that it generates a force which is repulsive and which is largest at very large distances. This force tends to drive the expansion of the Universe instead of opposing it. In this way the vacuum energy is unlike normal matter, which opposes the expansion. In particle physics it is a bit of a mystery why the vacuum energy is not a whole lot bigger than it is, but there are several mechanisms that might keep its size small. Eventually we may know which one works and why.
At very high density and temperature, as in the earliest Universe, particles are probably in a state in which they have zero rest mass. The process of changing out of this state as the Universe expands and cools may temporarily increase the cosmological constant, causing the Universe to expand very much more quickly than it was expanding to start with. Because the transformation to a nonzero-mass state would continually feed energy into the vacuum, the expansion rate would continually increase. The expansion of the Universe at a continually increasing rate is called "inflation." It is assumed that after the particles have completely attained their current rest masses, the inflation would end, although there are some technical difficulties in getting the theory to explain how the inflation would stop.
Because inflation can drive the expansion of the Universe so quickly, it can drive two points that were originally within each others' horizons out past the horizons. But since these two points were once inside each others' horizons, they were once able to equalize their densities. This quick expansion therefore allows two regions that are more than a horizon distance apart to have the same density without an appealing to an arbitrary specification of initial conditions. Hence we can use inflation to explain how the Universe we see can be so uniform. Inflation is the only known explanation for the uniformity of the Universe.
All known methods of driving inflation lead to a Universe which has a "critical" mass density. A Universe with a critical mass density expands forever, but it expands no faster than is required to just barely keep the expansion going. It is the need for inflation as an explanation of the uniformity of the Universe that leads us to choose critical density in calculating the age of the Universe. In fact, inflation is the only reason why we want the Universe to have the critical density.
What is observational evidence concerning the matter density of the universe? That question is worth a section of its own, so at this point read the section on Dark Matter.
For most of a star's life it has a stable brightness and color, while it obtains its energy by burning hydrogen into helium in its core. During this phase of their lives, all stars have brightnesses that are very closely related to their colors. When the hydrogen runs out, the star's atmosphere expands, its brightness increases slightly, and its color becomes much redder. Heavier stars have shorter lifetimes, and therefore begin getting redder much sooner than less-massive stars do. Heavier stars are also hotter and bluer. As the heaviest stars in a cluster start turning redder, the cluster has fewer and fewer hot, blue stars. As a result, a plot of brightness against color for the stars in a cluster can tell us how old the cluster is. A computer calculation is required to calibrate the ages, but the calculation is generally believed to be relatively reliable. In class we will show a computer program by Leos Ondra of the Czech Republic which shows the aging process for a typical globular cluster so that we can see how the ages of the clusters might be determined.
B. Chaboyer et al., in Science 271, 957 (Feb. 1996) have given carefully considered values for the ages of the globular clusters. According to a news article in Science 279 (Feb. 1998, p. 981), Chaboyer's current best estimate of the age of the oldest globular clusters is 11.5 +- 1.3 billion years. This age, plus the period required between the beginning of the Universe and the formation of globular clusters, sets a lower limit on the possible age of the Universe.
We have already defined the Hubble constant by looking at a diagram showing the recession velocity of galaxies as a function of their distance.

If one galaxy is twice as far away from us as a second galaxy, the first is moving away from us at roughly twice the speed of the second, so
velocity = H0 x distance
1/H0 = distance/velocity = Hubble time
For a number of years the observational evidence for the size of the Hubble constant has divided neatly into two sets of values. There has been little tendancy for newer observations to fall mostly in one set rather than in the other set, and only recently has there been a tendancy for the measurements to move to an agreed intermediate value. The news article in Science mentioned before quotes what are probably the best current values of the Hubble constant:
| Distance scale from | Hubble constant | Hubble time | |
|---|---|---|---|
| km/sec/Megaparsec | m/sec/ m (approx values) | billion years | |
| Cepheids | 73 +- 11 | 2.4 x 10-18 | 13 |
| "Nearby" Type IA supernovae | 58 +7/-8 | 1.9 x 10-18 | 17 |
| "Nearby" Type II supernovae | 73+-7 | 2.4 x 10-18 | 13 |
| Two Gravitational lenses | 63+-10 | 2.1 x 10-18 | 15 |
The Hubble constant implies the length of time the galaxies would have been travelling to get where they are now, and hence the lifetime of the Universe, only if the galaxies have been travelling at constant speed. Assuming that the uncertainty in the acceleration gives about a 33% uncertainty in the lifetime of the Universe, that lifetime would be 15 +-6 billion years. The lifetime of the Universe can be calculated using the Hubble time and General Relativity provided you know two things: the value of the cosmological constant and the current matter density of the Universe. Until very recently, there was very little data on the matter density of the Universe and none on the cosmological constant. The simplest, and therefore the preferred procedure, was to assume that the cosmological constant vanishes and that the matter density is that predicted by the theory of inflation (see above). The value given by inflation is the "critical mass density," which is defined by its effect on expansion: If the Universe had a mass density equal to the critical mass density and had a zero cosmological constant, it would expand forever; but if its mass density were any amount greater, it would eventually collapse back to high density. If we were to use these values for the two otherwise-undetermined parameters, the age of the Universe would be given by 2/3 of the inverse of H0 .
Using 2/3 for the parameter and taking 2.1 +- 0.3 x 10-18/sec as a combined value for the Hubble constant, the estimated value for the lifetime of the Universe is 10 +-3 billion years, rather uncomfortably close to the age of the globular clusters.
|
http://panisse.lbl.gov/public/papers/aasposter198dir/aaasposter.html
(Saul Perlmutter) |
Within the last two years new data has come in that, if confirmed, might completely change our understanding of the past and future of the Universe. The data come from observations of distant supernovae, and it indicates that the expansion of the universe is not constant in time but is in fact accelerated. These observations suggest that the cosmological constant is nonzero and are consistent with either a closed or an open Universe and with a Universe which recollapses as well as one which expands forever.
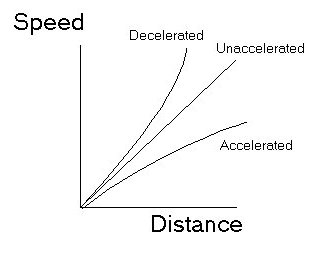
If the expansion of the Universe is accelerating, getting faster with time, then the increase of expansion velocity with distance gets larger as time goes on. The furthest galaxies are seen as they were a long time ago, due to the delay while their light is coming to our eyes. Hence we expect the the Hubble constant measured using only the furthest galaxies would be smaller than that measured using only nearby galaxies. Hence in the Hubble plot of speed against distance, the furthest galaxies will be below the straight line defined by nearby galaxies. Conversely, if the expansion is decelerating, getting slower with time, the galaxies that are furthest away will be above the straight line in the Hubble plot defined by the movement of the nearby galaxies. A rough and somewhat exagerrated plot of what we expect is shown below:
A careful calculation of effects of acceleration and the use of the Perlmutter et al. data on supernovae allow a determination of the most likely values of both the matter density of the Universe and the cosmological constant. The graph below is shown on the web page of the Supernova Cosmology Project and is included by permission of Dr. Saul Perlmutter. Note that it shows preliminary data and that the fully-analyzed data will be published later. The image has been reduced so that it will fit on a printed page; for a larger and better image click on the figure.
The diagram shows details of the favored values of matter density and cosmological constant. In particular, look at the right-hand side of the plot. [The horseshoe-like character is upper-case Greek omega, and the triangle with no base is upper-case Greek lambda, the cosmological constant. OmegaM is the mass density divided by the critical mass density (see below), and as stated, OmegaLambda is proportional to the cosmological constant.] The cosmological constant is most probably positive, although including systematic error a negative value is possible. The mass density is most likely between 20% of its critical density and just below its critical value. We will discuss measurements of the mass density in the next section of the notes.
If the cosmological constant is zero, the shape and expansion of the Universe is especially simple. If there is any matter in the Universe, the expansion must decelerate. Therefore the Hubble plot curves downward. For low mass density, the Universe is open and expands forever. At any given time, there is a largest mass density which is consistent with an indefinitely expanding Universe. This density is called the critical mass density. If the mass density is any higher, the Universe eventually recollapses. Mass also affects the average curvature of space. Below the critical mass density the Universe curvature is such that space is infinite in extent; above the critical density the curvature produces a finite Universe.
If the cosmological constant is not zero, relations get more complicated. For the purposes of expansion, the cosmological constant acts like negative matter: a positive lambda accelerates the Universe, and negative lambda decelerates it. However, lambda acts on the curvature of space in the same way that matter does: a positive lambda tends to increase the curvature of space, a negative value tends to decrease the curvature.
For the values of Lambda and Omega given by the supernova data, the value of the cosmological constant exerts the greatest effect on whether the Universe expands forever or the. The mass density is below critical, and for that density the Universe expands forever if the cosmological constant is positive and recollapses otherwise.
In general, there is a substantial trade-off between cosmological constant and mass density in determining whether the Universe is finite. A large positive cosmological constant can completely compensate for a low mass density, and a very negative cosmological constant can compensate for a high mass density.
The supernova data is consistent with either an open or a closed Universe. With the current estimate of the effect of systematic error, the data actually very slightly prefers a closed Universe, but basically the data is simply consistent with either possibility. The most likely values of the cosmological constant and mass density strongly favor a Universe that expands forever, but including the maximum likely effect of systematic error a recollapsing Universe is still possible.
| Next section | Previous section | End of section | Index of notes | Syllabus | Announcements |