|
| Next section | Previous section | End of section | Index of notes | Syllabus | Announcements |
|
| Next section | Previous section | End of section | Index of notes | Syllabus | Announcements |
| Last revised 1999/03/12 |
Quantum Mechanics describes the behavior of things that are very small. There are some major surprises when you start looking at the behavior of atomic nuclei, atoms themselves, and electrons or other subatomic particles. Experiments must now be explained in terms of probabilities, not certainties. The probabilities themselves are perfectly predictable (deterministic), so it is easy to find out almost exactly how large numbers of atoms will behave. However, it is not possible to determine exactly where in the overall pattern of events a particular atom will appear. The meaning of probabilities is perfectly illustrated by an old Reader's Digest story: An Alaskan trapper is asked if Grizzly Bears are really a problem in the backcountry. He replies that "99 out of 100 Grizzlies give you no problems at all. Of course they don't come in numerical order." In Quantum Mechanics you know pretty well the range of things that 100 electrons will do, but you don't know which one will do which thing.
The probabilities are wavelike, but the occurrences are localized. Hence atomic-scale objects do not act entirely like particles or entirely like waves. Because of the wavelike nature of the probabilities, it is not possible to determine the path that an atom took from one known point to another known point. As a result, for example, it is possible for a single electron or photon (particle of light) to pass through both of two isolated slits on a screen simultaneously.
In order to understand some of the details of quantum mechanics, we will examine closely one selected aspect of the behavior of waves so that we can recognize wave-like behavior. We will then talk about what happens if you look at the wave-like behavior of light very closely.
The Nature of Waves
A wave is a moving pattern. The pattern may be made up by any of a number of things: the metal rods on my demonstration machine, the molecules in the air in the case of sound, water in an ocean wave, electromagnetic fields in the case of light, and on and on. The things which make up the pattern are called the medium. The movement of the medium need not be the same as the movement of the wave. In the case of water waves (before they break on the shoreline), the movement of the water is mostly up and down even though the wave moves horizontally. In sound, the molecules move in the direction of the wave, but their position oscillates back and forth around a single spot. Over a full cycle the molecules do not go anywhere, even though the wave does. For light, the medium is composed of oscillating electric and magnetic forces which don't move at all; they just change their strengths. The class demonstration should give you a good picture of the difference between the behavior of the medium and the behavior of the wave.
Demonstration: the Wave Machine
Simple waves
In order to understand what happens when two waves overlap, we will think about a very simple wave: For half the cycle the particles in the medium will be slightly higher than they would have been in the absence of the wave. During the other half the particles will be low by the same amount. The diagram shows what I mean:

If we want to get a picture of the wave over a region, we can use green to show those spots where the medium is high and blue for those spots where the medium is low. A wave moving away from a point will then look like the diagram on the left. The various circles will expand with time. A bit later the wave might look like the diagram on the right.
Example:
This kind of wave may be seen by dropping a pebble in a puddle.
Interference
Adding waves
Now suppose we have two waves, but their high points are offset from
each other. The sum of the two waves is the sum of their heights at
any given point. If both of them are high, the sum is twice as
high. If both are low, the sum is twice as low. However, if one is
high and the other low, the two heights cancel each other and the
sum is zero.
We can see the effect in the diagram below, although not at a glance. There are two waves, one shown in blue-green and one in bluish red; their sum is shown in black. Trace out the green wave and the red wave with your eyes or a finger so that you can see exactly where each is. The green wave rises slightly to the left of the point where the red one rises. Now segment by segment verify that the height of the black wave is given by the sum of the heights of the green and red ones. Remember to subtract a height when it is below the zero point (the thinner black line marked with an "x").

There are two points to notice. First, the black wave has a pretty complicated shape. Second, there are places where the heights of both the green and the red waves are nonzero, but the height of the black wave vanishes. In fact, when two waves are moving in different directions, you can have spots where there is no movement at all. That is, it is possible to arrange things so that there are spots where either wave alone would move up and down but the sum of the waves is zero at all times. Such spots are called "nodes," and the existence of nodes is very important for the understanding of quantum mechanics. In class I will show this phenomenon on the wave machine.
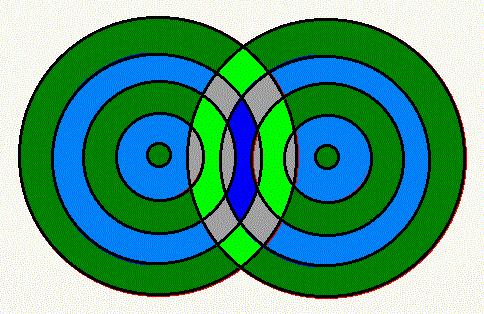
As the waves move outward, there will be little or even no
oscillation in the gray patches, and more oscillation where we are
showing bright green or deep blue. So where you see gray in this
diagram, there will be quiet areas with relatively small waves
compared to the areas around them.
Demonstration: Nodes on the wave machine
Demonstration: Laser and double slit
In class we will show the combination of two light waves using a small laser and a "double slit." The double slit is a dark slide with two narrow vertical lines cut very close together. When the laser shines on the slide, the two slits act like two close sources of light. By putting a screen in the path of the light, we can see where the waves are big and where they are small. There are some inessential mathematical complications due to the light moving mostly forwards instead of in all directions, so the slide also has a single slit that we can illuminate for comparison.
We will see that when we use a double slit there are dark areas on the screen that would have been bright if either slit alone had been used. In these areas, we must know that light has gone through both slits in order to predict correctly that the areas will be dark. The only way that the same light can go through both slits is if light is basically a wave. So...
Conclusion: Light must be a wave
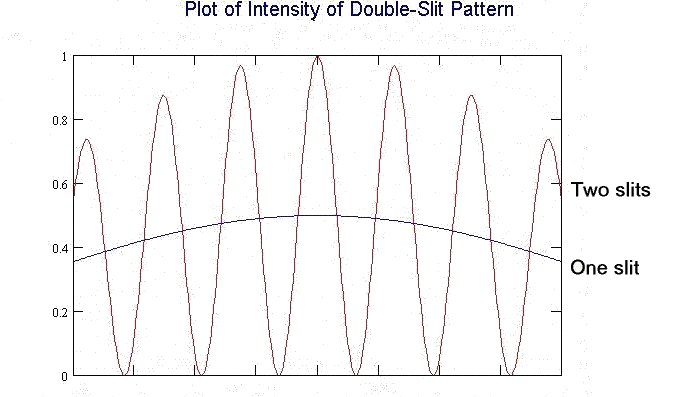
The line labelled "Two slits" shows the brightness of the light from the laser when it passes through two nearby slits. The horizontal axis represents where we are looking on the screen; the height of the line at any point gives the brightness of the light. The smoother line, labelled "One slit," is what the brightness would be if we added what we would see with only the left slit open to what we would see with only the right slit open. There are spots on the two-slit plot which are dark (zero brightness), for instance just left of the first hash mark at the bottom of the graph. The one-slit line shows that there would be light visible at that spot if the light passed through a single slit. We would see light there if the light came through either the right-hand or the left-hand slit. The fact that we get zero brightness from both slits and nonzero from either slit alone is our evidence that light is a wave.
Now think of turning the intensity of the laser gradually lower and lower. The pattern would get gradually fainter without changing shape. The peaks in the graph would get lower and lower without changing position. The lowest points would of course stay at zero, and they would not change position. Classically, these observations should go on forever, the pattern getting fainter and fainter and the curve getting correspondingly lower and lower.
However, in real life the process does not go on forever. Just as when you divide a metal into smaller and smaller bits you eventually obtain an indivisible atom or molecule, when you make the laser light less and less intense you eventually find individual flashes of light on the screen, which cannot be divided into smaller pieces. These indivisible bits of light are called photons. Photons are a new type of elementary particles to be added to the known electrons, protons, and neutrons.
Next question: where are the flashes? If they come in quickly, or if you sum them up for a long time, they must add together to give the interference pattern that we see when the light is brighter. They accomplish this by appearing more frequently where the interference pattern is bright and less frequently where the interference pattern is dark. Where the intensity of the light is zero, there are no flashes at all. But "they don't come in numerical order." You cannot use the position of the last flash to tell you anything at all about where the next flash will arrive. All you know is that when you have seen a lot of photons, more will have arrived at the spots where the light is bright than at the spots where the light is dim. It's a weird process; you see only a series of randomly placed flashes on various parts of the screen, but if you add up the number of flashes in each location you get a graph that looks like the interference pattern that we saw with the laser.
So, light comes to the screen as a series of particles, but if you add up the arrival positions the pattern is wavelike.
Terrible things have happened to our ability to make predictions. We cannot tell where any individual event (a flash) will happen, we only know where many events will occur. In other words, the wave pattern gives only the probability of the occurrence of events. We can calculate the probability quite deterministically and quite accurately. We cannot calculate the individual events. The world is fundamentally probabilistic.
Well, photons are strange beasts anyway, and we can perhaps live with using probabilities for them. Just so electrons and protons don't behave the same way.
Unfortunately, electrons, protons, and neutrons do behave exactly the same way that photons do. If you send a beam of electrons (or of one of the others) through a double slit of proper size, you will see interference patterns just like the one we saw on the screen using the laser. In fact, even if you send one electron at a time through a double slit, you will get an interference pattern. But electrons, like photons, arrive at localized spots. If you tabulate the locations, you build up the interference pattern. The wave properties of electrons in particular are responsible for the functioning of electron microscopes. All the elementary particles have wave properties just like the wave behavior of photons.
For either photons or electrons we can get into trouble if we try to describe what is going on too literally in English. For instance, which slit did the electron go through? Well.... Think about the dark spots on the screen. Remember that these spots would be bright if either slit were open alone. But no electrons land in those parts of the screen. Each electron "knows" that both slits are open, else some electrons would land in the spots that should be dark. In some sense, each electron has gone through both slits. Moreover, the pattern can be built up one electron at a time, so we cannot have one electron going through one slit, a second through the other slit, and then the two interfering with each other. It happens one electron at a time. In truth, it isn't meaningful to talk about the "path" the electron took. The entire wave is the electron, and the electron came along all possible paths.
The probabilistic nature of quantum mechanics actually allows us to make a prediction about forces. The argument that follows is more of a metaphor than a careful description of the mathematics. However, it is more right than wrong and so is worth knowing something about.
Forces in relativistic quantum mechanics are caused by the "exchange" of particles. Two particles that are exerting forces on each other are throwing spin-1 particles back and forth to each other. Weak forces are caused by the exchange of any of three particles of high mass called the W+, the W-, and the Z0 [the superscripts are the charges of the particles]. Electromagnetic forces are caused by the exchange of photons. Strong forces are caused by the exchange of one of 8 gluons. Gravity can be thought of as the exchange of a spin-2 particle called the graviton. It is possible, however, that gravity should not be thought of in this way; we don't know yet. There are no other known fundamental forces.
The particle to be exchanged could leave one of the participants in any direction and therefore land anywhere on a sphere whose radius is the distance to the other participant. The exchange can only take place, however, if the exchanged particle gets close enough to its target. Specifically, it must hit a fixed area centered on its target, and the likelihood of hitting that particular area A is larger if the area is larger. Any part of the sphere of a given size is equally likely, to the probability of hitting a particular target is given by the ratio of the area A of the target to the number of areas of the same size anywhere on the sphere. Hence the probability of the exchange is proportional to the area of the target divided by the area of a sphere whose radius is the same as the distance to the target. Since the area of a sphere is 4 pi times the square of the radius of the sphere, the probability of the exchange is proportional to A/(4 pi R2). [The number pi is the ratio of the circumference of a circle to its diameter.] Therefore we expect any fundamental force to have a factor of 1/R2 in the equation for its strength. That is, the strength of a fundamental force must fall off at least as fast as one divided by square of the distance between the two particles feeling the force. It can fall off faster than /1R2 if some of the particles disappear or turn around before getting to the target.
A particle leaving in any other direction is simply emitted with probability zero. In other words particles don't leave unless they are going to hit a target. The total probability of a force particle leaving is therefore not one.
For the forces given by the exchange of zero-mass particles, electromagnetic and gravitational forces, the 1/R2 factor is the entire dependence of the force on the distance. For weak forces, which are caused by the exchange of massive particles, there is an additional rapidly falling factor reflecting the mass of the exchanged particle. For strong forces, things are even more complicated. Gluons exert forces on each other as well as on most other particles. These forces have the effect of preventing gluons from getting very far away from other kinds of particles. Thus the strong forces vary as 1/R2 for two particles which are close together but are cut off abruptly at a distance of about the radius of a proton (10-15 meters).
I haven't explained the calculation of the intensity of the light along a screen after passing through a double slit. However, I found the curve by adding the wave-function of an electron going through the first slit to the wave-function corresponding to passing through the second, and then squaring the sum. Since equal parts of both wave-functions are included, an electron detected at the screen is equally likely to have passed through either slit. As we have said, the electron passed through both slits. There are other situations in quantum mechanics where a particle which classically would pick one only of several option may behave in a way showing that it followed all possible options instead. Such a particle is said to be in an "indefinite" state, to emphasize that we do not know "definitely" which option it followed. For example, if we scatter an electron off an atom, we may add internal energy to the atom at the expense of the kinetic energy of the electron. Classically, this either does or does not happen, depending on exactly where the electron passes. In quantum mechanics, energy may be randomly given or not given to the atom. We can predict the probability of the atom having one energy or another after the collision, but we cannot predict what its energy will be after any given collision. In this case we say that the atom has, say, a 50% chance of having its original energy and a 50% chance of having a higher energy. For short, the atom is 50% in the original "energy state" and 50% in the higher "energy state." This terminology eventually leads to the appearance that there are some logical paradoxes. These paradoxes are introduced by the language and are not present in the mathematics, but the language is used universally in the absence of any better way of saying things in English. The paradoxes are also usually taken seriously, unfortunately. [In fact, most physicists disagree with me about these paradoxes being artificial. I still think I am right. The issue is in any event a philosophical one, not a disagreement about the results of measurements. That is in fact why I feel that the paradoxes are artificial.]
In particle physics, there is a special case of this kind of "indefinite" state, where a property of a particle is not known. It is possible for some particles to be in states where we don't actually know what kind of particle they are. A particle created as a muon may later be a muon at some level of probability and an electron+neutrino+antineutrino with some different probability. The ambiguity comes about because there is a probability that the muon has decayed, but also a nonzero probability that it has not.
There are also a pair of spin-0 mesons, the K0 and its antiparticle, which can exist in a state with x% probability of being a K0 and (1-x)% probability of being an anti-K0. In fact, the simplest description of the decay of these two particles is in terms of the two states (K0 + anti-K0) and (K0 - anti-K0). This property of the K0 caused immense difficulty in puzzling out the relations among spin-0 mesons.
Another case involves the neutrinos. There are in fact three kinds of neutrinos, one that occurs in decays involving electrons, one associated with muons, and a third associated with an electron-like heavy particle called the tau. It may be (I believe it is) possible that neutrinos can exist in states where they are x% electron-neutrino, y% muon-neutrino, and (1-x-y)% tau-neutrino. Remember this possibility; it is the best escape from observations that otherwise would suggest that the sun has ceased making energy and will soon stop shining. Soon, that is, on astronomical time scales, say 10,000 years instead of the billion or so years that seems to be more likely.
The constant in question is called Planck's constant (strictly Planck's constant divided by 2 pi), and this statement is Heisenberg's Uncertainty Principle. A very large part of quantum mechanics can be understood semiquantitatively using this principle alone, without any fancy mathematics.
From here out, I am going to use the particle-physics convention of assuming that the angular momentum is internal and always calling it "spin," unless I definitely know otherwise. "Spin" is much easier to say than "angular momentum." Quantum Mechanics has much to say about spin. If the spin is not internal, the fact that we cannot really tell what path a particle is following must seriously affect the spin. The effect is to make it look like the direction of the spin is continually changing, so that the largest amount of spin in any given direction is not equal to the magnitude of the spin itself.
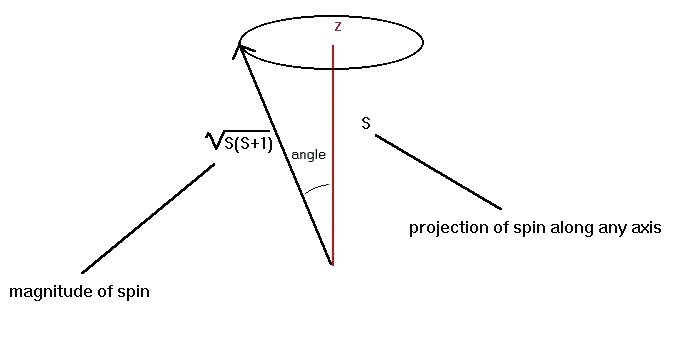
The diagram above shows the effect. The spin is on average pointing at an angle to the z-axis as shown on the diagram. We don't know exactly what angle the spin is along; we only know that it averages having the value shown. It is not, on average, aligned with the z-axis, so its projection along that axis is never sqrt[ S(S+1) ]. It can have a smaller average projection, but again never a set value. Only a few, discrete angles show up in the averages, so that the projection of the spin along the axis can be S, S-1, S-2, ..., -S+1, -S.
In addition, quantum mechanics provides a set of rules for adding spins. If two particles with spins occur together, the combination can have any of a set of spins. The rules are given below. Do not memorize these rules. If I ask you to use them, I will give them to you.
| 0 + S | = | S |
| 1/2 + 1/2 | = | 0 or 1 |
| 1/2 + 1 | = | 1/2 or 3/2 |
| 1 + 1 | = | 0 or 1 or 2 |
Reading from the table, if two spin-1/2 particles occur together, the combination may have either spin-0 or spin-1. No other values are possible. In particular, a spin-1/2 (3/2, 5/2, ...) combination must have an odd number of spin-1/2 parts and an integer-spin combination must have an even number of spin-1/2 parts. Any number of integer-spin parts can be included in these combinations without spoiling the rule.
There is one more interesting feature in quantum mechanics. Half-integer spins (1/2, 3/2, ...) involve a kind of internal spin only. They cannot be obtained by any combination of masses rotating around each other. True rotation involving actual movement always gives integer spin. Nonetheless, it is the combination of internal spin with rotation which is conserved (unchanged) in reactions, and not necessarily each type of spin separately.
| Next section | Previous section | End of section | Index of notes | Syllabus | Announcements |