|
| Next section | Previous section | End of section | Index of notes | Syllabus | Announcements |
|
| Next section | Previous section | End of section | Index of notes | Syllabus | Announcements |
| Last revised 1999/04/13 |
The addition of two spins is a bit complicated. For the lower values of J, the rules are
| 0 + n | = | n |
| 1/2 + 1/2 | = | 0 or 1 |
| 1/2 + 1/2 + 1/2 | = | 1/2 (two different ways) or 3/2 |
| 1/2 + 1 | = | 1/2 or 3/2 |
| 1 + 1 | = | 0 or 1 or 2 |
| 1/2 + 2 | = | 3/2 or 5/2 |
| 1 + 2 | = | 1 or 2 or 3 |
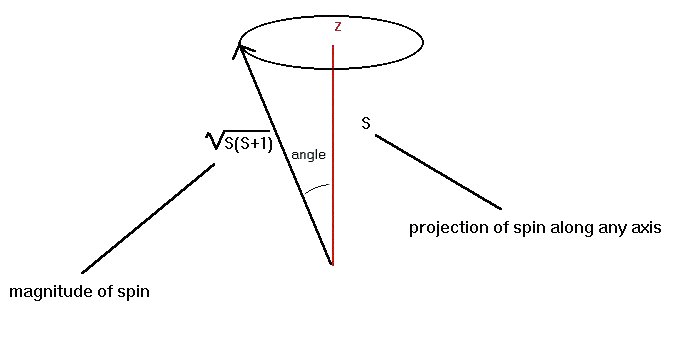
Since rotation involves an axis, and the axis has a direction, spin has an associated direction. In quantum mechanics, if the rotation axis were exactly in a set direction, the Uncertainty Principle would be violated, so the rotation axis itself must vary somewhat in position. The end result is that the projection of the spin (see the figure above) along any given direction is at most + J hbar and at least - J hbar. In between, the projections change by 1 hbar at a time, so that the projection of the spin (divided by h-bar) may be -J, -J+1, -J+2, ... +J-1, +J. For the first few values of J, the possibilities are
We can summarize the situation by saying that each particle of spin J, with J being an integer or a half-integer, has a spin of magnitude sqrt[(J (J + 1)] h-bar, and has 2 J + 1 possible spin projections ranging from - J h-bar to + J h-bar.
Our goal is to find out how various particles are related to each other and how to use the relations to group the particles into simple patterns. We will find labels, or quantum numbers, that will encapsulate the relationships. A quantity called isospin will be the first of these labels that we will locate.
At one time or another particle physicists have tried almost everything possible looking for patterns in the particle table. There are good formal (mathematical) reasons for expecting patterns to show up in the masses. In almost all of physics, energy is the most fundamental quantity to use to start building theories. In particle physics, the mass of the particle in its rest frame (that set of coordinates in which v=0) is related to the energy by Einstein's E=m c2, so particle physicists naturally looked hardest at mass relations. For us, not having the experience to feel that energy is all that important, looking at mass relations seems a bit arbitrary. So think of looking at all kinds of things, and abandoning the ones that don't work or don't work easily. Let's look at masses.
The next two graphs show the masses of the particles in the data table. There are two many to print conveniently in one figure, so I have split the graph into lower mass particles in the first part and higher mass particles in the second. The numbers along the bottom of the graphs are the charges of the individual particles.
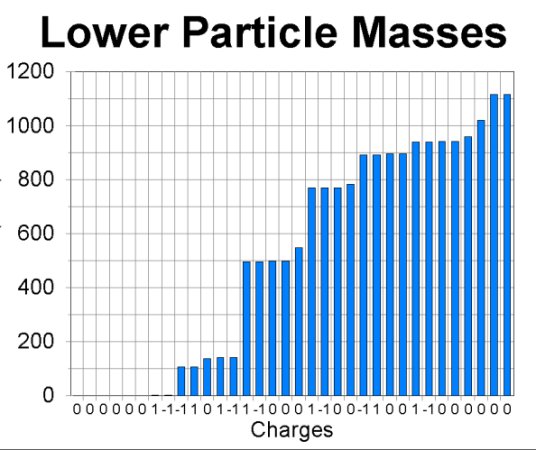
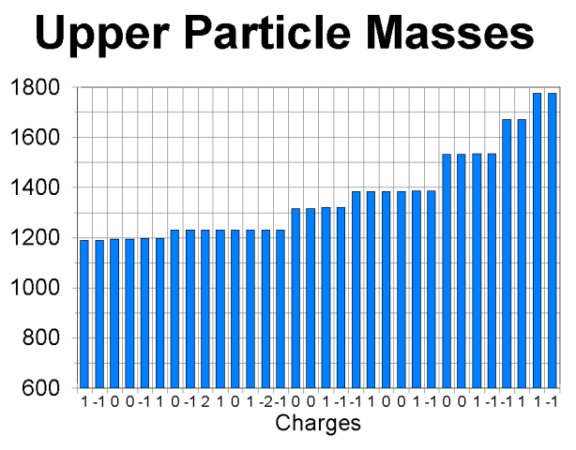
Now we already know a reason why two particles could have identical mass: they might be each others' antiparticles. If they are, there is nothing left to explain. The antiparticle relation is enough to make their masses the same. Since we are looking for additional relations, let us remove antiparticles from the picture, and plot a graph with only one of each particle-antiparticle pair included. At the same time, we will separate out the baryons, and postpone handling the other types of particles. The reason for this rather strange selection will become apparent as we go along. This graph is the next figure:
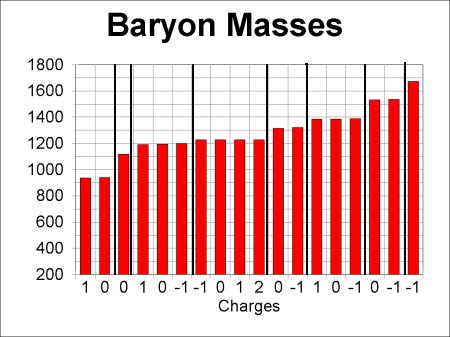
The heavy lines separate groups of particles whose individual masses clearly vary a lot less than the difference between the average masses of different groups. Notice that all particles within any given group have different charges. This property may indicate that we are on the right track, and permits us to list the members of the groups from smallest charge to largest charge. Call twice the average charge of a group by the symbol Y. Then we can construct the following table giving the charges of the various groups in the graph, starting from the left. Because the results are interesting, I have added a column to the table giving the spins of the particles in the table.
| Particles | Individual charges Q | Y=2Qave | Spin | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Proton, Neutron | 0 | +1 | 1 | 1/2 | ||||||
| Lambda | 0 | 0 | 1/2 | |||||||
| Sigma | -1 | 0 | +1 | 0 | 1/2 | |||||
| Delta | -1 | 0 | +1 | +2 | 1 | 3/2 | ||||
| Xi | -1 | 0 | -1 | 1/2 | ||||||
| Sigma* | -1 | 0 | +1 | 0 | 3/2 | |||||
| Xi* | -1 | 0 | -1 | 3/2 | ||||||
| Omega- | -1 | -2 | 3/2 | |||||||
A new pattern has shown up: all the particles that have similar masses also have the same spin. We got this simplification for free, so to speak, since we did not use spin in any way as a criterion for selecting the groups. We can also see that spin-3/2 particles tend to be more massive than spin-1/2 particles. We have, in fact, predictions about spins based on patterns in the masses, so maybe we are on the right track. It is in fact interesting to draw plots of the positions of baryons according to their charges (horizontally) and the average charge of the group they are in (vertically). Better results are obtained if we plot spin-1/2 and spin-3/2 baryons separately:

These diagrams are very nice, especially since they agree with patterns that can be predicted using a part of mathematics called group theory. At the time that Gell-Mann and Neeman first pointed out these results, the spin-3/2 baryon at the bottom of the triangle had not been seen. They predicted its existance and its mass, and it was soon found in an experiment at Brookhaven National Lab. The mass prediction was perfect.
The vertical axis of our graphs is usually labelled as hypercharge, Y, or strangeness, S. (Since strangeness steals the symbol S, spin is usually represented by J). The algebraic relations among average charge, Qave , hypercharge, and strangeness is
Qave = Y / 2
where B as usual is the baryon number. Along the horizontal axis, particles are labelled by a quantity called isospin, I, modelled after the behavior of spin. The group of particles with similar mass and the same hypercharge is called an isospin multiplet. The number of particles in the multiplet is given by
just as the number of possible spin states is given by N = 2 J + 1. We also define a "projection" of the isospin, called I3 , and label the members of the multiplet by values of I3 running from +I to -I, again just like the labelling of spin states. The charge of each member of the multiplet then becomes
The sets of particles that we have diagrammed are called SU(3) multiplets, after one of the objects described mathematically in group theory. In particular, the eight spin-1/2 baryons are called the octet and the ten spin-3/2 baryons are called the decuplet. Hypercharge was defined to agree with one of the quantities in group theory, and its name was chosen to reflect its relation to electric charge. "Hyper" simply distinguishes electric charge from the group-theory quantity and has no other meaning whatsoever. In particular, it has nothing to do with Star Trek's invented "hyperspace."
Why strangeness? Reactions in which the sum of the values of S after the reaction differs from the sum before uniformly procede more slowly than reactions in which the sum does not change during the reaction. Thus there is a "selection rule" for strangeness; changing strangeness slows down a decay or other kind of reaction. This fact was discovered before the pretty diagrams were discovered, and its definition was related to but not identical with the group-theory relations that were discovered later. Hence we have two quantities referring to basically the same property but defined in slightly different ways.
Isospin is defined the way it is because it is conserved in all strong interactions. It is in fact conserved in exactly the same way that spin is conserved, hence the analogous definition. It has no direct relation to spin (for instance, the sum of spin and isospin has no meaning) but the two separately follow the same mathematical behavior.
Unfortunately you need to know this terminology and have a sense of what quantities are related to each other. As usual, do not memorize the details of the mathematical formulas, but you should know that charge and isospin are related, the hypercharge and strangeness are related, etc. A good target would be to recognize that Q = I3 + Y could be correct but that Q = S + Y cannot be.
The first two options are very undesirable, as there is no indication that particles and antiparticles should be treated this differently. The third option is not much better, leaving some of the mesons out of the patterns altogether, but it should probably be looked at. The fourth option is undesirable as well, since it would count some particles twice. The fifth looks strange but doesn't really violate any esthetic arguments. In principle we should probably look at all of them (except maybe #1 and #2) to see how they work out.
I will do the fifth option first since it is the one that actually works. Hence the diagram below contains all the mesons, both particles and antiparticles:
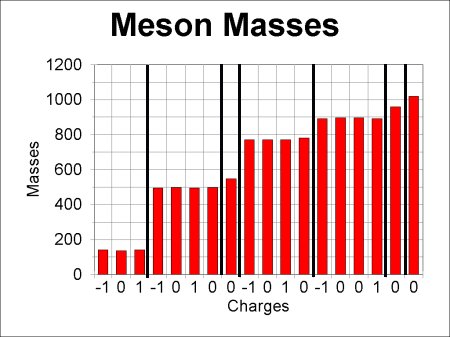
I will include the strangeness of these mesons when I tabulate what is in the graph; the values are determined by analyzing the speeds of the decays of the mesons. I will not for the moment tabulate Y. The resulting table has a few surprises:
| Particles | Individual charges Q | Spin | Strangeness | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| pi | -1 | 0 | +1 | 0 | 0 | |||||
| K | -1 | 0,0 | +1 | 0 | +1 and -1 | |||||
| eta | 0 | 0 | 0 | |||||||
| 3 rhos and 1 omega | -1 | 0,0 | +1 | 1 | 0 | |||||
| K* | -1 | 0,0 | +1 | 1 | +1 and -1 | |||||
| eta' | 0 | 0 | 0 | |||||||
| phi | 0 | 1 | 0 | |||||||
Three of the groups that have similar masses contain two chargeless particles, which did not happen with baryons. We cannot describe these groups as a simple isospin multiplet. However, in two of these cases [K, K*] the particles also do not all have the same strangeness, and it is natural to see what happens if we insist that the members of the group all have the same strangeness as well as nearly the same mass.
The remaining case (rho, omega) is more difficult. It takes a detailed study of several decay modes of these particles to determine for certain that two different isospin multiplets are involved. It turns out that there are, and that the near-agreement in mass between the three rhos and the omega is somewhat accidental.
If we implement these changes in the table to see if we get something compelling, we get the following results. In this table I will not try to keep the groups in strict mass order, instead making the table look as much like the baryon table as I can.
| Particles | Individual charges Q | Spin | Strangeness | Y=2Qave | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| K | 0 | +1 | 0 | 1 | 1 | ||||||
| pi | -1 | 0 | +1 | 0 | 0 | 0 | |||||
| K | -1 | 0 | 0 | -1 | -1 | ||||||
| eta | 0 | 0 | 0 | 0 | |||||||
| eta' | 0 | 0 | 0 | 0 | |||||||
| K* | 0 | +1 | 1 | -1 | -1 | ||||||
| rho | -1 | 0 | +1 | 1 | 0 | 0 | |||||
| K* | -1 | 0 | 1 | -1 | -1 | ||||||
| phi | 0 | 1 | 0 | 0 | |||||||
| omega | 0 | 1 | 0 | 0 | |||||||
Several nice things have happened, in addition to what we forced to happen:
A plot of the mesons is given below:

The net result of all this analysis is that we have discovered that mesons can be placed in groups, two of which have quantum numbers that are like those of the spin-1/2 baryons, and two of which consist of a single member each (singlets). The two singlets may seem like a failure of the analysis to cover all the possibilities, but we will see shortly that in fact they fit in perfectly.
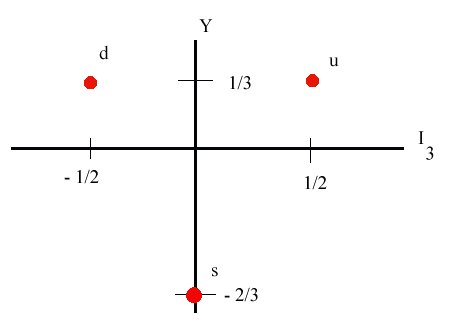
The three quarks are usually called the up quark, the down quark, and the strange quark, and are so labelled in the diagram above. Group theory suggests that baryons would be made up of three quarks, antibaryons of three antiquarks, and (matter) mesons of one quark and one antiquark. The distinction between matter mesons and force-carrying mesons is now precise: matter mesons are those which are composed of quarks.
The tables below show the quark content of the baryons and mesons. It is difficult to show how to get these with a static text, but we will go through the construction in class. We will also show how to figure out what the quantum numbers of the quarks must be. You need to know these procedures, so you should be expecially sure to be in class for these constructions.
For the spin-1/2 baryons, the results are
|
|
For the spin-3/2 baryons, the scheme is
|
|
The spin-0 and spin-1 mesons have the same quark structure. We show the names of the spin-0's. For the spin-1's, replace pi by rho, eta by phi, and put asterisks on the K's:
|
|
In addition, the singlets eta' and omega have quark content s anti-s (to good approximation).
Single quarks are never observed, and in the course of figuring out these quark contents of baryons and mesons, we will find that we need a way to forbid the presence of systems containing any net number of quarks other than a multiple of 3 as well. We will define a quantity whimsically called color to do the job. After the class discussion of color I will attempt to put some helpful discussion into these notes at this point, but again I think that this topic is most easily handled in class.
Further quarks have been discovered. They were named the charm, bottom (some use beauty) and top (some say truth instead) quarks. A table of the properties of quarks and leptons, listed side by side, shows interesting features:
| Generation | Q=+2/3 Quark | Q=-1/3 Quark | Q=0 Lepton (Neutrino) | Q=-1 lepton |
|---|---|---|---|---|
| 3 | top | bottom | tau neutrino | tau |
| 2 | charmed | strange | muon neutrino | muon |
| 1 | up | down | electron neutrino | electron |
There is a similar table of antiquarks and antileptons, of course. This table clearly suggests that there is some kind of similarity between quarks and leptons, but no one has been able to find a consistent theory of "subquarks" or symmetry relations that makes correct predictions. Hopefully, some experiment sometime will shed light on the structure.
| Next section | Previous section | End of section | Index of notes | Syllabus | Announcements |