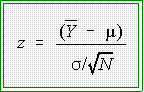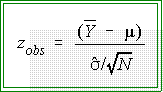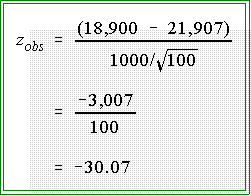DEPARTMENT OF POLITICAL SCIENCE
AND
INTERNATIONAL RELATIONS
Posc/Uapp 815
TEST OF MEANS

- AGENDA:
- Test of a mean.
- Overview
- Sampling distribution: standard normal
- Critical values and regions
- One-tailed and two-tailed tests
- Reading:
- Agresti and Finlay, Statistical Methods, Chapter 6:
- Read pages 155 to 159 for general ideas regarding hypothesis
testing.
- Read pages 1159 to 167 for test of the mean procedures.
- ANOTHER EXAMPLE OF THE BINOMIAL:
- This section repeats the notes from
Class 23.
- Problem: a population of available jurors in a city contains 53 percent of the
population who do not favor capital punishment. This is known from a detailed
public opinion survey. A local judge is suspected of approving only potential jurors
who favor the death penalty. The last jury consisting of 12 people which dealt with
a murder case contained only 5 people who said they opposed capital punishment.
Is there any evidence of selective bias?
- Hypotheses:
- The "research" hypothesis is that the judge is biased which means that the
proportion of "anti-capital punishment jurors" will be less than .53. Thus,
the HA (HA is the alternative hypothesis.)
- The null hypothesis is P =.53.
- The H0 asserts that a population parameter
equals a specific value.
- Since the alternative hypothesis (HA) is that P is less than .53 we will
consider only those sample results at the "low" end of the scale as
disconfirming evidence. This is a one-tailed test of significance. (See
below.)
- Sampling distribution and critical region:
- Let us decide ahead of time that we will consider any sample result
that occurs with probability less than .02 as evidence that the null
hypothesis should not be accepted.
- The sampling distribution and critical region and critical values for
this problem are shown in the figure on the next page. Note that N
= 12 and P = .53:

- Given the nature of the problem, we will reject the null hypothesis only if
we get, say, 0 or 1 or 2 "anti-capital punishment" jurors; that is, we will
use only one tail of the sampling distribution to test the hypothesis.
- Sometimes when there is no clear alternative hypothesis we will consider
unlikely events at both ends of the distribution.
- Critical value: we have agreed ahead of time
to reject the H0 if a sample
result occurs with probability of .02 or less. Thus, from the above
distribution we see that the critical region includes outcomes 0, 1, and 2.
The outcome 3 occurs with probability .0367 and is therefore above the
critical value.
- Hence the decision rule is: reject H0 if and only if Y, the number of
"successes," is 2 or less.
- The level of significance is therefore .02.
- Sample result: the data indicate that Y = 5 jurors oppose capital
punishment. The sample result is thus 5 which we compare with the
critical value.
- Decision: since 5 is greater than 2 (the critical value) we do not reject the
null hypothesis.
- Interpretation: We have concluded that the judge is not biased against
jurors who oppose the death penalty. There is a chance that we have made
a mistake, but this time the possible error is in failing to reject a null
hypothesis that should be rejected.
- THE TEST OF A MEAN - OVERVIEW:
- The hypothesis is that ,
the population mean, equals a specific value.
- This is a large sample test: N must be at least 75 or larger.
- The sampling distribution is the standard normal
- That is, sample statistics will be converted to standard scores (you have
already done this) and compared to a standard normal critical value
- The standard deviation of the sampling distribution is called the standard error of
the mean. It is often denoted
 .
.
- In effect, we will calculate a sample z and compare it with a critical z.
- Review:
- You should review the material pertaining to the standard normal
distribution, the mean, and the standard deviation.
- Reviewing these notes on your own may also be helpful. This material is
not at first sight obvious but with a little work it can be mastered.
- LARGE SAMPLE TEST OF MEAN:
- Problem: George Easterbrook writes: "Farm families as a group are not poor.
Their average income in 1983, one of the worst years in memory for agriculture,
was $21,907." Yet a sample of 100 tax returns from farm families across the
country shows the average family income to be $18,900 with a standard deviation
of $1,000. Given that you have a great deal of confidence in the independence of
the sample, the data support Easterbrook's contention that farm family income is
$21,907?
- Assumptions and requirements: we assume that the sample is SRS and that there
are at least 75 cases. (In this problem that requirement is met because N = 100.) If
the sample is less than 75 another procedure is used, as we will discuss in a coming
class.
- Hypotheses:
- The research hypothesis (HA)is that
m is less than $21,907 because we
suspect that the stated value is too high.
- That is, HA: m < $21,907
- The null hypothesis (H0) is, however,
m = $21,907.
- Sampling Distribution:
- If repeated samples of size N are drawn from a
population having a mean
and variance s2,
then as N becomes
large the sampling distribution of the
sample means,
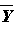 ,
becomes normal with mean and standard
deviation
,
becomes normal with mean and standard
deviation
 .
(The standard deviation of the sampling distribution is called the standard
error of the mean. See below.)
.
(The standard deviation of the sampling distribution is called the standard
error of the mean. See below.)
- In words, suppose we take a sample of size N = 100 from a population
with a mean of m = 500 and
standard deviation of s = 50.
Using these 100
cases we calculate the mean (average) of the data with the usual formula.
(That is we calculate
the
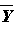 for this particular sample.)
Now suppose we
obtain a second, independent sample of 100 and do the same thing; that is,
get a
second
for this particular sample.)
Now suppose we
obtain a second, independent sample of 100 and do the same thing; that is,
get a
second 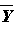 Then we repeat the process another time and another and
another...each time calculating a sample
mean
Then we repeat the process another time and another and
another...each time calculating a sample
mean 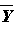 If we kept on doing this
thousands and thousands of times what would the collection of sample
means look like? How would they be distributed? What would a
stem-and-leaf display show? What would the mean of the means be?
If we kept on doing this
thousands and thousands of times what would the collection of sample
means look like? How would they be distributed? What would a
stem-and-leaf display show? What would the mean of the means be?
- The answer, given by statistical theory, is that these means would
have a normal distribution, the mean of which would be the
population mean (m = 500 in this case),
but the standard deviation
would be not sigma, the population standard deviation, but rather
sigma divided by the square root of N.
The standard deviation of
the sample means would be:
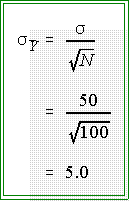
- Figure 2 on the next page shows a general picture of the theoretical
sampling distribution.
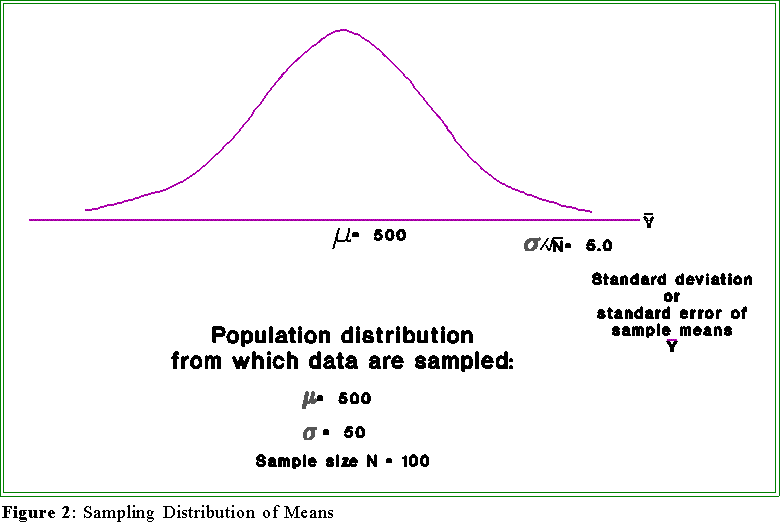
- The distribution of sample means is
normal with a standard deviation (called the
standard error of the mean or simply the standard error) equal to sigma
divided by the square root of N.
- Thus, if we are dealing with sample means based on relatively large N's
(more than 75) the appropriate sampling distribution is the normal
distribution.
- Remember, a sampling distribution is used to show the probability of
obtaining a particular sample result or one even more unlikely. Knowing
that sample means have a normal distribution allows us to use our
knowledge of the normal distribution to make inferences about the
likelihood of a particular sample mean occurring, given that the
hypothesized population mean is such and such.
- Furthermore, we found that we can always convert raw data to
standardized data so that we can use a "tabulated" standard normal
distribution. (See below.)
- In the present problem, the hypothesized population mean is $21,907 whereas the
sample mean is $18,900. Using the standardized normal distribution as the
sampling distribution allows us to say whether the sample result could have arisen
by chance (given the null hypothesis) or whether it is such an unlikely event that
we want to reject the null hypothesis.
- To use the standard normal distribution one must convert raw data--here the
sample mean--to a standardized or z score.
- The formula for doing so is this:
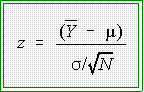
- To use this formula one has to
know s,
the population standard deviation
which is unknown so we estimate it
by using
 ,
the sample standard
deviation. Now the formula for getting an observed z is:
,
the sample standard
deviation. Now the formula for getting an observed z is:

- The quantity,
 is called the standard error of the mean. It is interpreted
as the standard deviation of the sampling distribution of the mean.
is called the standard error of the mean. It is interpreted
as the standard deviation of the sampling distribution of the mean.
- Before leaving the topic let's look at the standard error of the mean a bit
more.
- Suppose sigma, the population standard deviation, equals 100 and N is
relatively small, say 10. Then if we take repeated samples of size N = 10,
calculate a
 each time,
and plot the result we will get a figure that looks
something like the previous figure.
each time,
and plot the result we will get a figure that looks
something like the previous figure.
- Now suppose we do the same thing--take repeated samples and get sample
means
 but this time use much larger sample sizes, say N = 100. The
result would be a normal distribution with mean , but a smaller standard
deviation.
but this time use much larger sample sizes, say N = 100. The
result would be a normal distribution with mean , but a smaller standard
deviation.
- What is going on is this: each time we take a sample from a population
with a mean of
and s = 100 and
calculate
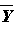 the observed sample mean
will not equally exactly the "true" value because of sampling error.
Sometimes
the observed sample mean
will not equally exactly the "true" value because of sampling error.
Sometimes 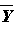 be too large, sometimes it will be too small, and only
very, very rarely will it equal the true value. But over the long run, the
average of the averages, so to speak, will equal the population mean.
Hence, we say the expected value of sample
means,
be too large, sometimes it will be too small, and only
very, very rarely will it equal the true value. But over the long run, the
average of the averages, so to speak, will equal the population mean.
Hence, we say the expected value of sample
means, 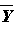 equals the
population mean, m . In symbols,
equals the
population mean, m . In symbols,
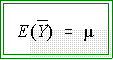
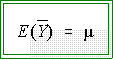
- This is read as "the expected (long run) value of sample means
equals the population mean from which the samples are drawn.
- Note in addition this important fact, which may be intuitively clear: as the
sample sizes get larger and larger, the sample means should come closer
and closer to the true value, although in most instances they will not equal
it. That is, if you have a sample of 5,
your sample
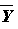 may be quite far from
the true value, but if you increase your sample to 1,000 then
the
may be quite far from
the true value, but if you increase your sample to 1,000 then
the 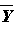 will in all
likelihood be quite close to the true value. This idea is reflected in the
standard errors of the sampling distributions: when N is only 5
the
will in all
likelihood be quite close to the true value. This idea is reflected in the
standard errors of the sampling distributions: when N is only 5
the
 tend
to be scattered widely above and below the true value, but when N is 1000
the
tend
to be scattered widely above and below the true value, but when N is 1000
the
 (which are guesses)
about the true value tend to be bunched close
together. You can have more "confidence" in a sample mean based on 1000
cases than on one based on just 5 observations. But note:
(which are guesses)
about the true value tend to be bunched close
together. You can have more "confidence" in a sample mean based on 1000
cases than on one based on just 5 observations. But note:
holds no matter what the sample size.
In other words, small samples are
just as "valid" as large ones--their expected values equal the true
parameters--but they do not give you as much confidence because any
particular value of a small sample might be quite far from the true mean.
- Look carefully at the formula for the standard error and you can see this
concept even more clearly: for a given sigma (the population standard
deviation) as N increases the denominator of the formula increases and the
standard error decreases. Here are a few examples:

- We see that as N increases the standard deviation of the sampling
distribution (called, remember, the standard error) decreases. This makes
sense because the variability of sample estimates of should be less when
the sample is based on 1,000 or 10,000 cases.
- Level of significance and critical region:
- Suppose we want the level of significance to be .05. The level of
significance, you will recall, is the probability of making a Type I error--of
incorrectly rejecting the null hypothesis.
- Our job then is to find a critical value which will define a critical region of
such a size that the probability of falling into it is .05, given of course that
the null hypothesis is true.
- Since we are dealing with a normal distribution, however, we know how to
find values that mark off various portions of the curve or distribution.
Consider the familiar picture:

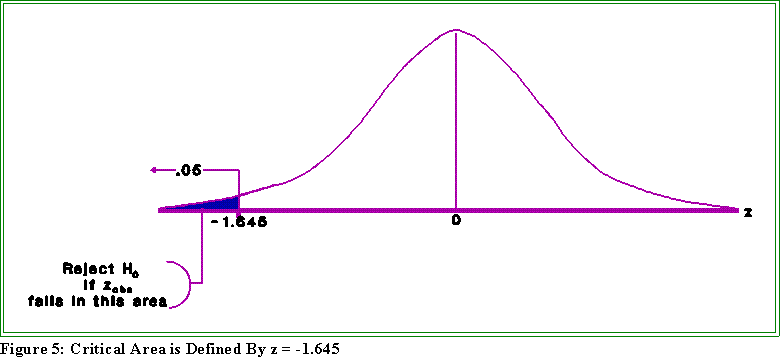
- To find the critical value, locate the z from the table of the standard normal that
corresponds to .5 - .05 = .45. It is about 1.645. Since we are looking at the left
side of the curve the critical value is actually minus 1.645.
- Figure 5 shows the idea:
- The question is now: does the sample mean ($18,900) when
converted to a standardized z score fall into the critical region.
That is, is the observed z
based on
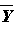 greater
than or equal to the
absolute value of the critical z? If so, reject the null hypothesis; if
not accept it.
greater
than or equal to the
absolute value of the critical z? If so, reject the null hypothesis; if
not accept it.
- Test statistic:
- To calculate the test statistic convert the
observed
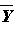 ($18,900) to a
standard score. You know how to do this except that since we are dealing
with a sampling distribution we use the standard error,
denoted
($18,900) to a
standard score. You know how to do this except that since we are dealing
with a sampling distribution we use the standard error,
denoted , instead
of the standard deviation. The formula is:
, instead
of the standard deviation. The formula is:
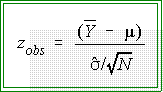
- For this problem the observed z is:
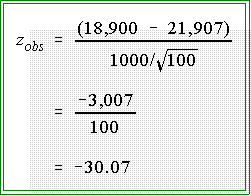
- The observed z is thus -30.07
- Decision:
- Since the absolute value of the observed z is very much greater than the
absolute value of the critical z we reject the null hypothesis.
- Interpretation:
- It appears that the Easterbrook's assertion about farm income is incorrect:
in fact, it may be much less than he suggests.
- Given that we have not accepted the H0 our best estimate of the true value
is now $18,900.
- After rejecting a null hypothesis, you should try to make an estimate of
what the true value is. In the case of sample means,
the value
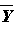 is an
"unbiased" estimator of m.
is an
"unbiased" estimator of m.
- NEXT TIME:
- More on tests of means and proportions.

 Go to Statistics main page
Go to Statistics main page
 Go
to H. T. Reynolds page.
Go
to H. T. Reynolds page.
Copyright © 1997 H. T. Reynolds