DEPARTMENT OF POLITICAL SCIENCE
AND
INTERNATIONAL AFFAIRS
Posc/Uapp 815
REGRESSION ANALYSIS
Further Topics

- AGENDA:
- Summary of regression and correlation so far
- Examples of regression analysis
- Reading:
- Continue Agresti and Finlay, Statistical Methods, Chapter 9 material on
regression.
- For now skim the material on "significance" and "hypothesis
testing"
- SUMMARY:
- Regression model

- b
is the unstandardized linear regression coefficient:
- Indicates nature or direction (positive or negative) of a linear
relationship.
- A one unit change in X (whatever a one unit change means) is
associated with b units change in Y.
- b
is measured in units of Y.
- Magnitude partly determined by measurement scales.
- Asymmetric: regression of Y on X is usually not the same as
regression of X on Y.
- Know or at least be willing to specify one of the variables as
dependent.
- a
is the unstandardized regression constant.
- It indicates the (hypothetical) value of Y when X is zero.
- Alternatively, stated it is the expected value of Y when X is
zero.
- Measured in units of Y.
- R2, the (multiple) regression coefficient
- Interpretation: the amount of total variation in Y that X "explains."
- Use: one indicator of how well the linear regression model "fits" the data.
- Properties:
- Always has a value between 0 and 1.0.
- Negative R2 is not possible. (After all, how could one explain less
than 0 percent of the variation.
- If R2 = 1.0, then X "explains" all of the total variation in Y.
- It cannot exceed 1.0 because (intuitively) how can one
variable explain more than 100 percent of the variation in
another.
- The "bounds" (0 and 1.0) are also easily seen from the formula for
explained variation.
- The correlation coefficient, r.
- Also a measure of how well data "fit" a linear model.
- Or, interpret it as a measure or index of linear correlation.
- Bounds: -1.0 to 1.0.
- 1.0 suggests a perfect positive correlation between X and Y; -1.0 indicates
a perfect negative correlation.
- r = 0 suggests that X and Y are not linearly correlated.
- Note: this does not mean the variables are statistically independent.
- It's a symmetric measure: the correlation taking X as independent equals
the correlation taking Y as independent.
- Variation in X and/or Y can affect the numerical value of r.
- See below for an example of this important property.
- Cautions:
- It is difficult to measure "theoretical" importance with any single statistic.
- By themselves R2 and r do not necessarily show that one variable,
X say, is a more important correlate or explanation of Y than is, say
Z.
- Further remarks on r.
- The correlation coefficient's "size" in a given context depends on the
"strength" or degree of correlation and the amount of variation in the
variables as can be seen in the following very hypothetical data sets. (See
Figures 1 and 2 that are attached to the notes.)
- In Figure 1
the range of X values is relatively limited.
- The pattern of data points plus the estimated least squares line
suggests no linear correlation between X and Y.
- But suppose one collected more data on a wider "variety" of cases
that had more or wider variation in X.
(See Figure 2)
- What's the difference between these two figures? The first is a
subset of data drawn from the first. Since the range or variation in
X is rather narrow, however, the apparent correlation between the
variables is nil. But by collecting data in such a way as to increase
variation in X, one sees that there really is a linear relationship
- The moral: maximize variation on the explanatory variable as much as
possible.
- Example: suppose you collected data in one country or region of a
country. It is entirely possible that the range of X values is relatively
limited. If so, your conclusions about the effects of X on Y could
be misleading in the sense that although they apply for the
population under investigation, they would not hold for a different
population.
- So substantive conclusions based on statistical evidence have to
take account not only of differing conditions, but also the variation
in the independent and dependent variables.
- Data collected in different times and/or in different places may or
may not be comparable. Always look at variation.
- Least squares estimators.
- See the notes for Class 18
- For more on the principle of least squares see Agresti and Finlay, Statistical
Methods, pages 313 to 314.
- Interpreting regression "output."
- See notes for Class 18.
- Look for "coefficients" (unstandardized) and R2
- To find the correlation coefficient use (in MINITAB) Statistics, Basic
Statistics, and the Correlation.
- Simply enter a list of variable names or column locations and the
program will produce a "correlation matrix," r's between all pairs
of variables in the list.
- NOTE ON NOTATION:
- Up until this point I have been a little sloppy with the notation.
- Keep in mind, however, that I (and others) generally hold to the conventions we
have been discussing, namely population parameters are denoted by Greek letters,
such as b,
where as sample estimators of these quantities are denoted with a "hat"
over the corresponding symbol.
- Since putting the hat on the symbols is a pain in the neck, I don't always do
so. But the context should indicate whether the statistic refers to a sample
or population value.
- To be consistent one should denote the population correlation coefficient with the
Greek letter for lower case r; that is, r. But the usual convention is to use r,
instead of r with a hat over it to represent a sample estimator. I will follow that
convention r
- REGRESSION EXAMPLES:
- Surgical procedures.
- See the notes for Class 18
for the background.
- First consider the relationship between the number of surgical specialists in
a state and the number of operations performed (per capita).
- See the plot.
- Regression results for complete data; that is, batch includes the District of
Columbia.
- Here is the estimated equation:
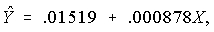 where X
is number of surgical specialists per 1,000 population.
where X
is number of surgical specialists per 1,000 population.
- Since R2 = .406, one would assume that this linear model fits the
data quite well.
- See the second plot.
- What might be the conclusion? The more surgeons, the more
operations are performed. So the policy implication is perhaps to
cap somehow fees or limit the number of surgeons.
- Alternatively, one might ask if surgeons aren't follow "need." That
is, there might the large number of surgical specialists might simply
reflect the need for them; they "migrate" or set up practice in areas
that require their services and not elsewhere.
- But before accepting any of these hypotheses and the policy
implications they carry, look once more at the plot. Note that one
point, the District of Columbia stands out from the others in the
sense that its X value is way above average.
- You can check this for yourselves simply by scanning the
data or better by drawing or obtaining a box-and-whisker
plot.
- One of the drawbacks of OLS regression and the correlation
coefficient is that they are "sensitive" very large/small values.
- That is, their numerical values can be greatly affected by a
single value that is quite "far" from the mean of X.
- To see the effects of this outlier look at the
figure
and consider the
regression equation when it (D.C., the "outlier") has been removed.
- Now the regression equation is:
see the
equation at the topic of the figure.
- Recall what was said about measurement scales and the interpretation of
the regression coefficient.
- In the first equation it was .0008; in the second it is .0001.
- These may "look" similar but in the context of the problem there
not since the first is 8 times as large as the second.
- So the first model suggests that a 1 surgeon increase per 1,000
population would be associated with .0008 increase in surgical
procedures. But suppose the number of surgeons increased by 100.
Multiple .0008 by 100 to get .08, or .08 surgical procedures per
capita.
- Now examine the second coefficient, the one calculated when the
outlying case has been removed. It (.0001) suggests that if the
number of surgeons increased by 100, the number of procedures
would only increase .01 or 8 times less than in the other case.
- If you looked at a 1,000 surgeon increase, the difference in
coefficients would be even more apparent.
- Look also at the second R2: it's .005.
That indicates that X now (with D.C.
removed) explains .005 time 100 = .5 percent of the variation in Y. In other
words by eliminating a single case, we have reduced the "explained"
variation from about 40% to less than one percent.
- This result explains why one has to be cautious when interpreting statistics.
In fact, the lesson is to use as much information, graphs and so on, as
possible.
- Which model is correct? I suspect most people would say the second
because it seems to include only "typical" data.
- For practice you might retrieve these data from the web site (be sure to create a
variable "procedures per capita," as I have done) and do the analysis with the other
independent variable, number of general surgeons per 1,000 population.
- ADDITIONAL EXAMPLES:
- If time allows we will consider more examples of regression analysis and perhaps
ways to retrieve data from the "internet" and analyze them with statistical
software.
- FILE TYPES:
- If time, some discussion of file types and what to do.
- File types can be identified by their "extensions" the three characters at the ends of
their names:
- .txt: ASCII: text and/or data (alphanumeric)
- .dat: data (numbers) files
- .xls: Excel file format.
- .wk?: Lotus 1-2-3 file format.
- .dbf: dBase file format
- .sps: SPSS file format.
- MINITAB (the full version) can "import" all of these file types except for SPSS.
- Import means that a program can "read" or convert the data into a form it
recognizes.
- The "Student Version for Windows" also imports many of them.
- Use "open worksheet" dialog box.
- It may be necessary to remove text from the worksheet, however.
- It is also possible to "export" data into many of these data types
- Similarly, SPSS can import most of these file types except MINITAB.
- To move or convert from SPSS to MINITAB (or vice versa) save data as an
ASCII file and then read them with the other program.
- Another commonly encountered type is "portable document file" format ("pdf").
- These text and graphics files must be read with "Acrobat," a free software
program that can usually be obtained from the place that makes the files
available.
- Many government reports are distributed in this format.
- Word "processing" programs such as WordPerfect and Word can be used to "cut"
columns of data.
- Read or open the file.
- When using Word place the insertion point at the start of a column and
hold down the "ALT" key.
- Move to the last row of the column to highlight the data. Use the
"Copy" on the Edit menu to copy the column to the clipboard.
- Then open a new file (either another Word document or a Notepad
file) and paste the numbers.
- Save as a text file.
- WordPerfect works essentially the same way except use the Edit, Select,
and Rectangle menu.
- Experiment; once you get the idea you can copy sections of data
relatively easily.
- NEXT TIME:
- Further discussion of regression
- Multiple regression
- "Dummy variable" regression
- "Intervention" analysis: regression with time series data.

 Go to Statistics main page
Go to Statistics main page
 Go
to H. T. Reynolds page.
Go
to H. T. Reynolds page.
Copyright © 1997 H. T. Reynolds
