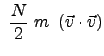 |
|||
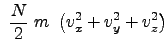 |
|||
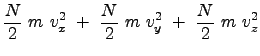 |
|||
In 3-D, for a collection of many particles (on the order of Avogadro number), using average values of velocity and velocity components (in Cartesian coordinates); these are not generalized coordinates (as physicists would consider), the total kinetic energy is:
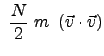 |
|||
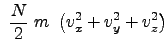 |
|||
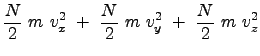 |
|||
The last equality is really just a notational trick; there really does not exist a thermodynamic
or kinetic property ![]() or
or ![]() or
or ![]() !
The lowercase
!
The lowercase ![]() is mass.
is mass.
The velocity is a vector so the ![]() we treat casually is really a dot product.
we treat casually is really a dot product.
The pressure components for the x , y , and z directions as we determined in class are:
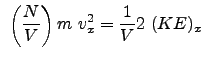 |
|||
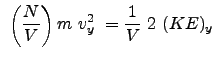 |
|||
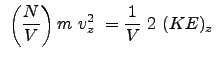 |
From statistical mechanics (which you will learn more about in the future) we have the relation for the special case of a fluid or state of matter with extremely weak interactions (or no interactions):
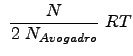 |
|||
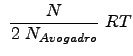 |
|||
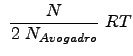 |
Thus,
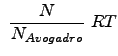 |
|||
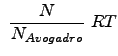 |
|||
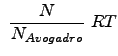 |
Substituting the above relations for ![]() , etc. into the pressure equations yields:
, etc. into the pressure equations yields:
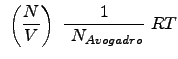 |
|||
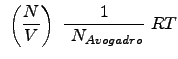 |
|||
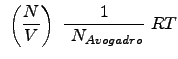 |
Recall that
![]() is the number of moles
is the number of moles ![]() . Thus, the equations for pressure
become:
. Thus, the equations for pressure
become:
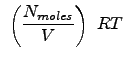 |
|||
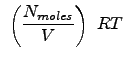 |
|||
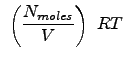 |
Here, we stop and realize that we have a x-component of pressure, a y-component and a z-component. This is not an artificial result, as rigorously, pressure is a tensorial property (it is a 3x3 matrix). The diagonal elements (which we have computed) have special meaning in that they can be used to determine the pressure as we know it. Rigorously, the scalar pressure (that we normally measure and talk about) is determined from the trace of the pressure tensor (or matrix). This is:
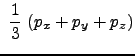 |
|||
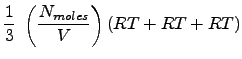 |
|||
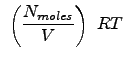 |
|||
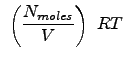 |
This should be a more convincing argument for the equality of kinetic theory description of fluids to that of an ideal gas.