University of Delaware

PHYS146

Quarks, Gluons, and the Big Bang

Maurice Barnhill
Next section Previous section End of section Index of notes Syllabus Announcements
Last revised 1999/01/19

Class Notes III. Expansion of the Universe

Outline of Hawking Chapter 3
The Expanding Universe

(Compare pp. 8-9 of Chapter 1)

  1. The Expansion of the Universe (pp. 35-46)
    1. Other galaxies
    2. Spectra of stars
    3. Doppler effect
    4. Expansion: most galaxies are moving away
    5. The Cosmic Microwave Background
    6. Friedmann Models of the Universe
    7. Density of the Universe
  2. The Beginning of Time (pp. 46-51)
    1. Friedmann-model singularity at t=0
    2. Steady-State Model [no t=0]
    3. Lifshitz-Khalatnikov calculation
    4. Proof that Friedmann models have a singularity at t=0

Outline of Class Notes III

  1. Velocities of galaxies
    1. How can we tell how fast a galaxy is moving?
      1. Stellar and galactic spectra (compare text pp. 37-38.)
      2. Spectra from moving bodies (compare text pp. 38-39)
  2. Distance scales [from notes by Strobel, previously available on WWW]
    1. Solar System distances
    2. Parallaxes
    3. Evolution of clusters
    4. Cepheids
    5. Standard galactic features
  3. Plotting velocity against distance (compare text pp. 39-40)
  4. The Big Bang (Compare the Friedmann-model discussion in the text, pp. 42-45)
    1. Extrapolation back
    2. Initial density and temperature
    3. Cosmic radiation (compare text pp. 41-42)

Velocities of galaxies

Stars are made up of compressed, hot gas containing several different kinds of atoms. Gasses that are hot enough glow, giving off light and heat. Both light and heat are a type of wave, and the color of the light is determined by the frequency (or wavelength) of the wave. Under the conditions present in the bodies of stars, all possible colors are radiated. The atmospheres of stars are, however, cooler and less dense. Under the conditions in the atmospheres it is possible to see the radiation of individual colors characteristic of individual elements. In class I will show how these spectral lines for Neon and Sodium. Since the stellar atmosphere is cooler than the star behind it, the atoms in the atmosphere do not radiate as brightly as the surface of the star does. When you look at the sun in the particular color given off by an individual atom, you see a cooler gas and therefore darker color. Between those colors, you see all the way to the surface and see a hotter gas and a brighter color. As a result, at the color where a given chemical element in the star's atmosphere is radiating, we see a relatively dim light compared to nearby colors. Use a prism to spread the light into a spectrum, and the colors where we see dim light look like a set of dark lines against a bright background. Those lines are of course not really dark, just dark by contrast with the surrounding colors. Seen alone, without the background of the very bright stellar surface, those lines would look very bright indeed.

A set of stellar spectra is available from the University of California at Irvine. The codes on the left are labels for the stars whose spectra are shown; the numbers at the bottom are the wavelength scale in Angstroms.

Since the color of these lines is known if the element is known, and vice versa, we can tell by looking at the spectrum what the wavelength of any given line was when it left the atom. We can also measure directly what the wavelength is when we see it. We will now show that these two lengths do not have to be the same and that their difference tells us how fast the star is moving.

Using a simple piece of apparatus, I will show in class what waves look like and how they behave. A particularly simple wave is shown here in the figure below.

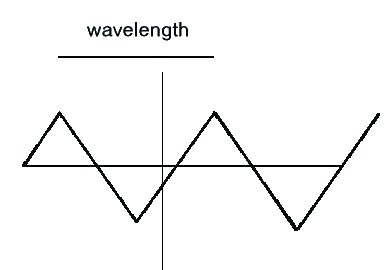
The wavelength, the distance between two peaks of the wave, is marked on the diagram. In the rest of the diagrams in this section, we will show only the location of the peaks of the wave. We will call the peaks "wavefronts." The speed of the wave is given by how fast the positions of the wavefronts change with time.

We would like to show what happens to a wave when its source is moving away from us. To do this, we show in the figure below the locations of a black ball and a red ball at various times, showing their positions horizontally and the times vertically. (If you are looking at the diagram in black and white, the black ball is on the left and the red one on the right.)

We will show what is happening at three different times: 0 seconds, 1 second, and 2 seconds. The graph looks like a strip of movie film taken at at rate of 1 frame per sec. The black ball is not moving, so it is at the same horizontal position all three times. However, the red ball is moving to the right and accordingly will be at a different position at each time. We are standing on the far left, so the red ball is moving away from us and the black ball is stationary.

At time zero, at the bottom of the graph, wavefronts are given off by both the black and the red ball. Each wavefront moves towards us, and we show where they are at all three times.

The bar on the left side of the graph shows how far the black wavefront has moved between times zero and one second. There are two bars on the right side. The lower bar shows how far the red wavefront has moved and the upper bar shows how far the red ball has moved. Obviously the total distance between the ball and the wave is the sum of these two distances. Notice that the black and red wavefronts have moved the same distance in this time interval, so they are moving at the same speed, as light would do.

The distance between the red wavefronts is the sum of the distances that the wavefront and the ball have moved, which will make the wavelength of the red light longer than that of the black. To see that the distance is longer, we add some more wavefronts to the diagram. At one second, the middle of the diagram, wavefronts are given off by each ball. These wavefronts move towards us, and we show where they are at one second and at two seconds:

Notice that the new black and red wavefronts have moved the same distance in this time interval, so they are moving at the same speed. They are also moving at the same speed as the wavefronts in the previous diagram.

In the next diagram we show both the wavefronts emitted at t=0 and those emitted at t=1. We also add the next wavefronts, emitted at t=2 seconds:

Look at the distance between wavefronts at t = 1 second or t = 2 seconds. The red wavefronts are clearly further apart than the black ones. When the source of a wave is moving away, the distance between wavefronts (the wavelength) is longer.

In the case of light, that longer wavelength means that the light is redder. Hence if a body is giving off light at a known frequency, we can determine how fast it is moving by measuring the wavelength of the light.

How does this phenomenon help us? We can look at the spectrum of a galaxy, which, remember, is full of absorption lines with wavelengths which are known when the source of the line is at rest. We can measure the wavelengths of the lines in the galactic spectrum, usually finding numbers that are different from those measured in the laboratory. The difference in wavelength tells us how fast the galaxy is moving. We can then seek patterns in the speeds of the galaxies. However, it turns out that to find patterns we must also know the distance of each galaxy from us. So now we must see how to find out how far away a given galaxy is.

Distance scales

In this section I am following fairly closely the notes by Strobel.
  1. On the Earth
    Here distances are simple. We compare the distance between any two objects to the length of a standard rod (a meter stick). Sometimes the comparison is a bit indirect. If we can't lay sticks out directly, we can measure off a baseline, measure the change in direction to the object from each end of the baseline, and determine the distance by "triangulation."

  2. Solar System distances
    The relative distances of planets, asteroids, comets, etc., can be determined by using Newton's Law of Gravity. However, one absolute distance from the Earth to another object is needed. The old way to get this one distance was to look at the changing direction to a nearby object as you moved from one point on the Earth to another. This is called the parallax method and was applied to the moon or a nearby asteroid. Now we can get the distance to the Moon and Venus directly using radar. Either way we determine indirectly the actual distance from one side of the Earth's orbit to the other.

  3. Parallaxes
    Knowing the distance across the Earth's orbit, we can use the change in direction to the nearest stars from one side of the orbit to the other to determine the distances to stars in the neighborhood of the Sun. Measure the direction to a star, then wait six months until the earth is on the other side of the sun and measure the direction to the same star again. Since we are looking at the star from different locations, the direction will change slightly. The two directions and the known diameter of the earth's orbit form the base and two angles of a triangle, from which we can determine the height of the triangle, and that height is just the distance to the star. If the star is too far away, there is no visible change in direction, and the method fails, but the technique is foolproof for the nearest stars.

  4. Evolution of clusters
    Studying the nearby stars, we find that the brightness of stars varies systematically with color. The coolest stars are red, orange stars are a bit brighter, followed by yellow, white, blue, and blue-violet stars. If we could look at a star's color and determine its brightness, we could use its actual brightness and apparent brightness to determine its distance. Unfortunately, for any given color there are a range of brightnesses, governed primarily by the age of the star. Thus we can't look at an individual star and determine its actual brightness by measuring its color.

    However, there are many groups of stars clustered in the same place which are found to all be of the same age. The pattern of brightness vs. color in these clusters can be used to determine the cluster's age, and knowing the age we know the brightness of the stars in the cluster.

    There are more such clusters at distances which we could not measure directly. We can determine the ages of these clusters and from the age and color the actual brightness of the stars in the cluster. Hence we can tell the distance to these clusters despite not being able to measure it directly.

  5. Cepheids
    As we look at clusters that are further and further away, their apparent size gets smaller and smaller. Eventually the individual stars are (apparently) too close together to see separately, and we are no longer able to determine the distance to the cluster. So there is a limit to how far we can measure distances by the cluster method.

    Some of the clusters whose distances can be determined have stars in them which vary in brightness, getting gradually brighter and fainter on a regular schedule. A recognizable set of these variable stars, the Cepheids, vary on a time scale which is closely determined by their brightness. Stars of the same type occur outside clusters where they are not obscured by their neighbors. We can use the known actual brightness of any Cepheid we find to determine its distance. This method works as far as the nearest galaxies. Using the Hubble Space Telescope, we are getting distances out to the nearest clusters of galaxies. Beyond that distance, we can't find the Cepheids against the background of the other stars in the galaxy, and a different method is neaded.

  6. Distant Supernovae
    The best measure of long distances seems to be the peak brightness of certain supernovae (exploding stars), called Type 1A Supernovae. The system that blows up consists of a small and very dense star called a white dwarf paired with a largish conventional star. The white dwarf is the remnant of a star that has used up the nuclear fuel that provides stars with their energies. After running out of fuel a star, if not too massive, collapses to very high density, and the resulting object is called a white dwarf. If the white dwarf has a companion which is so nearby that some of the gas from the larger star is pulled over to the white dwarf, then eventually the white dwarf gets so much mass that it collapses completely, leading to a very large explosion. The exploding star can be as bright as the entire galaxy it is in! The best part for us is that the explosion always occurs when the white dwarf gets to a specific size, so the explosions all have the same brightness.

    Of course, nothing is quite that simple, and there are variations in the brightness of the Type 1A Supernova explosions. However, observations of Type 1A Supernovae at known distances indicate that the form of the decline of their brightness after the explosion tells you which supernovae were brighter than average and which less. Hence observing the amount of light put out over a period of days or months will tell you the absolute brightness of the supernova. From its intrinsic and apparent brightnesses, you can as usual figure out how far away the supernova must be. Moreover, you can see supernovae a long way away due to their very high intrinsic brightness.

    Data on Type 1A Supernovae at large distances are now being collected by at least two research groups. This data implies that very distant galaxies are moving away from us even faster than you would expect from the data on relatively nearby galaxies that we will show below. Near the end of the course, we will talk more about the implications of such an "accelerated expansion" towards the end of the semester.

In summary, we can determine the distance to the nearest galaxies rather well. We can also determine the distance to galaxies further away with rapidly improving accuracy.

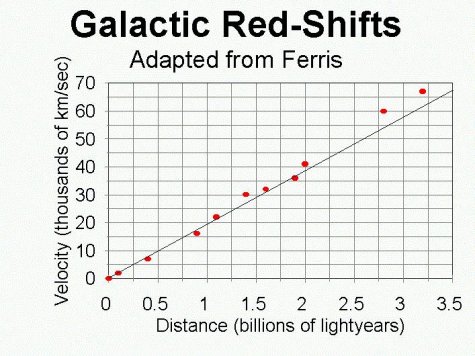
Plotting velocity against distance

Now we can combine our knowledge of the velocities and distances of many galaxies, seeing if there is any pattern. The easiest way to do this is to make a graph showing velocity on the vertical axis and distance on the horizontal axis. An adaptation of a figure from Timothy Ferris, Coming of Age in the Milky Way is shown immediately below. All the velocities are directed away from us. This plot does not show the most recent, most distant data. Those galaxies would fall near the plotted line but apparently on average somewhat below the line.

Clearly the further away a galaxy is the faster it is moving away from us. In fact, you can predict the velocity by the relation

velocity = H0 x distance .

If you compare the velocity of one galaxy with that of another galaxy twice as far away, the further galaxy has twice the velocity. The number (H0) which, when multiplied by the distance to a galaxy gives its velocity, is called Hubble's constant. The quantity 1/H0 gives an estimate of the age of the universe, as we will discuss in the next section. The value of H0 given from the graph above is about 60 thousand km/sec per billion lightyears, or about 2 x 10-19 m/sec / m , implying a lifetime for the universe of around 10 billion years.

Don't think that we are picked out as being special by having all the galaxies moving away from us. The situation looks exactly the same from any other galaxy as well. I will try to show how that works during the lecture. To try the demo yourself, print out the the "view of the universe" both before and after a 20% expansion, put the two pages on top of each other and hold them up against a strong light. Make the two circles with dots in them (us) sit on top of each other and see how all the circles have moved further away from us as the universe expanded. Now choose another pair of circles to sit on top of each other and see how all the other circles have moved away from that point during the expansion. Continue until you are convinced. [This is not my original idea. I found the suggestion in a newsgroup and have unfortunately forgotten who invented it.]

One more weird point. If the universe is infinite in size, the movement of all the galaxies apart from each other is not making the universe larger. There doesn't have to be a place where galaxies are moving into "empty space." The universe is getting much less dense, but it is not necessarily getting larger. Twice infinity is still infinity.

It might be easier to understand the infinite universe expanding without getting larger from a fictional example. Consider a hotel with an infinite number of rooms, 1, 2, 3, 4, ..., all occupied. An infinite number of potential customers show up, asking for rooms in the hotel. The desk clerk says, "Sure, no problem." What does he have in mind?

To get the rooms he needs, the desk clerk calls all his patrons up and asks them to change rooms to that he can house more clients. He puts the current occupant of room 1 into room 2, that of room 2 into room 4, and so on, like this:

Previous 1 2 3 4 5 6 ...
Now   2   4   6   8   10   12   ...
Leaving vacant 1   3   5   7   9   11   13 ...

An infinite number of rooms, the odd-numbered ones, are vacant, and he puts the new customers in them. Problem solved.

The Big Bang

Now if all these galaxies are moving away from each other, where did they come from? In the past, they must have been much closer together. If you think back far enough, much closer together. So close together there wasn't room for the empty spaces between galaxies or even between stars, and the whole universe was filled with a dense gas of atoms. Earlier than that there wasn't even room for the empty space in atoms, and the universe was a soup of protons, neutrons, electrons, neutrinos, and photons. Earlier even than that we don't yet know enough particle physics to handle, so we will have wait until later in the semester to understand what was there.

As the universe expands from this early, dense state, it must cool, as any expanding gas cools. The universe is now pretty cold (about 3 degrees Centigrade above absolute zero), but it has been cooling a long time. At the stage when it was a gas of elementary particles it must have been very hot indeed.

If you stand near a campfire the part of your skin facing the fire feels hot, even if the wind is blowing from you to the fire. Incandescent light bulbs give off both light and heat. In fact, all things that are hot give off radiation. The coolest give off just infrared, and as a body gets hotter it glows red, yellow, white, blue, ultraviolet, and at the hottest temperatures radiates even beyond the ultraviolet. All of this radiation is really a gas of photons moving around at the speed of light, sometimes getting absorbed when they hit something else. The ones that are absorbed are replaced by others being given off by the hot bodies.

In the early universe, the hot protons, electrons, etc., give off many photons because of their high temperature. At the same time they absorb many photons, making a unified gas of protons, electrons, and photons. As the universe expands, the protons and electrons form atoms, which also absorb and emit photons, making a gas of atoms and photons. The universe expands further, lowering the density of atoms. Eventually the density of atoms is low enough that not many photons find atoms to absorb them, and the photons become an independent part of the gas. Eventually many of the atoms in the gas collect together to make galaxies and the objects within galaxies, but the photons continue to fly around unimpeded. The gas of photons, now separate from the atoms, is of course also expanding and therefore cooling. At the current age of the universe, the temperature of the photon gas is 3 degrees K (3 degrees Centigrade above absolute zero). At this low a temperature the photons correspond to microwave radiation, and can be detected by ultrasensitive radio receivers. The detection of this "microwave background" is a very direct piece of evidence for the statement that the early universe was hot and dense.

The photons in the microwave background have come to us directly from the earliest moments of the universe. They therefore carry information about the structure of the universe near its beginning. We will use this information in future weeks to learn what the early universe was like. Particle physics will turn out to play a crucial role in the behavior of the early universe.

Next section Previous section Beginning of section Index of notes Syllabus Announcements