|
| Next section | Previous section | End of section | Index of notes | Syllabus | Announcements |
|
| Next section | Previous section | End of section | Index of notes | Syllabus | Announcements |
| Last revised 1999/01/19 |
Some elementary particles have been known for a long time. Light and other forms of electromagnetic radiation are carried by photons, which has been known since the early days of quantum mechanics. Later we will look at the arguments for photons in some detail. Protons, neutrons, and electrons are known from chemistry. Atoms are all made up of a cloud of electrons around a positively-charged nucleus consisting of protons and neutrons. It is worth looking at the logic that leads to the conclusion that nuclei are composite, since we will later want to apply similar arguments to the proton and neutron themselves.
Using data from the American Institute of Physics Handbook (McGraw Hill, New York) of 1957, pages 8-56 to 8-62, we can compile a table of masses of the least massive nuclei. In the table, the mass unit is 1.67 x 10 -27 kilograms, the charge unit is 1.60 x 10 -19 Coulombs, and I have chosen arbitrary names. A kilogram is a mass that would weigh about 2.2 pounds on the earth's surface. The expression 1.0 x 10 -27 means "write down 1.0 and move the decimal point 27 places to the left"; 10 +27 would mean moving the decimal point 27 places to the right. Hence a particle of "approximate mass" 1 in the table would weigh about 3.67 x 10 -27 pounds. It would take slightly fewer than 300,000,000,000,000,000,000,000,000 [26 zeros] of such particles to weigh a single pound. If at the beginning of the universe you had started counting the particles of mass=1 that make up a pound of material, counting one per second, you would now be 1 ten-billionth of the way through the job. Atomic nuclei are not very heavy.
|
|
It isn't so easy to see what is going on from a table of data alone!
[What is going on? Do you remember?] It is much easier to
understand if we draw a picture. Let's draw a vertical line (axis)
with equally-spaced marks labelled 1, 2, ..., 8. Each step along
this line can represent an additional mass of one unit. We can draw
another horizontal line with marks representing charge. Each step
along this line will represent an additional charge of one unit. Now for
each one of the nuclei in the table, place a dot lined up with the
place on the vertical axis corresponding to its mass and also lined
up with the place on the horizontal axis corresponding to its
charge, like so:
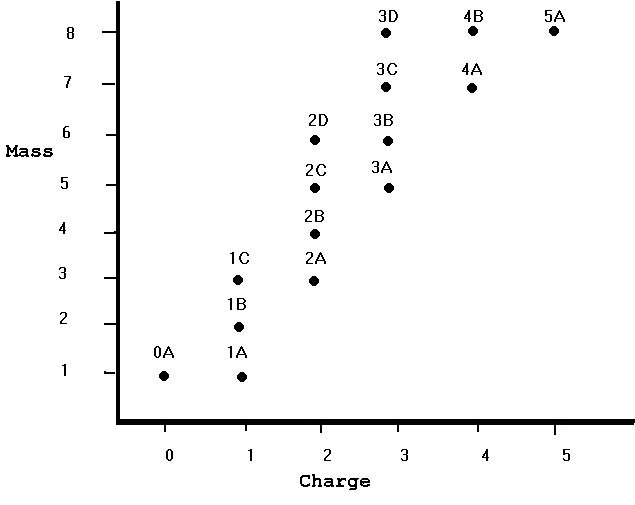
You can also see that the dots are not scattered over the entire graph. Most of the dots are in a diagonal band through the center of the graph. Although there is room on the graph for 5 different nuclei of any given integer mass, there are in fact only 3 nuclei of mass 8, 2 of mass 7, 2 of mass 6, and so on. There is in fact only 1 nucleus with mass 2.
The number of nuclei of a given charge and different mass are also (necessarily, given the previous paragraph less than the possible number of eight. There is only 1 0-charge nucleus, 3 charge-1 nuclei, etc. As the charge goes up, the minimum mass tends to go up also. The fact that there is only one charge-5 nucleus might be due to my not having presented any data for mass greater than 8, which is the minimum mass for charge 5. You might even want to predict that there are more charge-5 nuclei with masses greater than 8.
Finally, what makes this data so simple? Well, "nucleus" 0A is the neutron, and 1A is the proton. All the others are made up of some number of protons and a possibly-different number of neutrons. The mass of the nucleus is the sum of the masses of its protons and neutrons, hence basically the total number of protons and neutrons. The charge of the nucleus is the sum of the charges of its constituents, and since the neutron is neutral the total charge is the same as the number of protons. In particular, 1B is made up of one proton and one neutron and has a mass of 2 and a charge of 1; 5A is made up of 5 protons and 3 neutrons and has a mass of 8 and a charge of 5. The diagonal band of existing nuclei is due to forces that break nuclei up too quickly for them to be seen if the number of protons is very different from the number of neutrons. If there too many protons, their mutual repulsion by electric forces tears the nucleus apart. If there are too many neutrons, two things can happen. Either some of the neutrons turn into protons, changing the makeup of the nucleus, or the nucleus is too large for nuclear forces to hold it together.
So now we have nuclei composed of protons and neutrons, and a problem understanding how to keep the nuclei intact in the face of repulsive electrical forces between the protons. There has to be some other force counteracting the electrical forces (also called Coulomb forces). The new force is called the strong force (or sometimes the nuclear force). It acts only over short distances, so if nuclei get too big it becomes less effective than the long-range Coulomb forces. It was surmised that three particles called pions were responsible for the strong forces, much as the attraction that keeps some molecules together is generated by sharing electrons between the atoms in the molecule. Eventually particles with all the right properties to be pions were driven out of the nucleus by energetic atomic collisions, confirming the existance and role of the pions. Since then our understanding of strong forces has advanced, and pions are not considered to be fundamental force carriers, but their role in nuclei is almost exactly what was originally surmised.
Measurable properties of particles
Elementary particles have surprisingly few measurable properties. In this section I will explain the meaining of several of these properties. In some cases a complete explanation will have to be postponed until we go through some background material. When a property of a particle can be described by a single integer or simple fraction, it is frequently called a quantum number. There are a few quantum numbers that I will not attempt to explain until some additional background is available.
Like macroscopic objects, particles can have energy and momentum. You can't, however, use either one directly to tell you what kind of particle you are dealing with, since all particles can have many different energies and momenta. Since we are interested in characterizing the particles, we will not deal with energy and momentum very often.
Mass: The mass of a particle, just like the mass of a macroscopic object, tells how easy or hard it is to change the objects velocity. To be precise, if a the amount that the velocity changes each second under a force F, then
However, it is almost always impossible to measure the mass of a particle from this definition. Instead, Einstein's equation E=Mc2 is used to turn energy measurements into a measurement of the mass. Here c is the speed of light.
Charge: The charge of a particle determines the size of electromagnetic forces exerted on or by that particle. The exact relation is that the force exerted by a particle of charge Q1 on another particle of charge Q2 (or vice versa) is given by
where r is the distance between the charges and k is a constant we can look up when we need it. The important point is that if you double the charge without changing the distance, you double the force. Forces on charges can be measured, although somewhat indirectly, so the charge of a particle can be easily measured as well.
Spin: Any body that revolves around another or that rotates around an internal axis is said to have angular momentum. The amount of angular momentum is proportional to the speed of revolution or rotation and to the mass of the body, and the amount depends on the distribution of the mass around the axis of revolution/rotation as well. Under many circumstances the amount of angular momentum in a complete system of particles does not change with time. If the angular momentum comes completely from rotation about an internal axis, it is frequently called spin. A complication of quantum mechanics is that there is also a spin which contributes to the angular momentum of an elementary particle but which does not represent an internal rotation. This quantity is called intrinsic spin and acts exactly the same way that it would if it were really caused by an internal rotation. The intrinsic spin of a particle is one of the variables that distinguishes what kind a particle you are viewing. Spin can be measured in units that make the spin of a proton or an electron exactly 1/2. In these units, quantum mechanics requires that all spins be 0, an integer, or half an odd integer. We will work almost entirely with small spins: 0, 1/2, 1, 3/2, and 2.
Lifetime: Most particles eventually disappear, leaving behind two or more particles whose masses are less than that of the original particle. This process is called decay. It takes place with a characteristic average lifetime, meaning that if you have a number of the original particles at a given time, after one lifetime half of them will have decayed. The particles left after the decay are called decay products and the set of of decay products is a decay mode. Particles which do not decay are called stable. Most unstable particles have more than one possible decay mode, some of which may be much more common than others. In the Particle Table I have listed one or two of the most common decay modes, but there are usually many that I have left out. The lifetime does not refer to any one decay mode but rather is the time required for half the particles to decay by any mode whatsoever. The decay is caused by some force or another, and the length of the lifetime and the liklihood of any particular decay mode gives a clue as to which force is responsible for that mode.
[Scattering]
For the particles we have so far, the simpler properties are listed in the table below. For a more complete table with more particles, see the Particle Table.
| Particle | Mass | Charge | Spin | Lifetime |
|---|---|---|---|---|
| Photon | 0 | 0 | 1 | stable |
| Electron | 0.511 MeV | -1 | 1/2 | stable |
| Pi 0 | 135 MeV | 0 | 0 | 8.40 x 10 -17 sec |
| Pi + | 140 MeV | +1 | 0 | 2.60 x 10 -8 sec |
| Pi - | 140 MeV | -1 | 0 | 2.60 x 10 -8 sec |
| Proton | 938 MeV | +1 | 1/2 | stable |
| Neutron | 940 MeV | 0 | 1/2 | 887 sec |
The charge and spin are given in units in which the proton charge is +1 and spin is 1/2. I will explain the meaning of "MeV" as a mass unit later. In more familiar units, the proton has a mass of 1.67 x 10 -27 kg. [For gosh sakes don't memorize these numbers!] Notice that the superscripts on the word Pi give the charges of the pions. This convention is used quite frequently and saves much time looking up charges in tables.
| Next section | Previous section | End of section | Index of notes | Syllabus | Announcements |