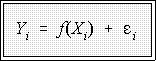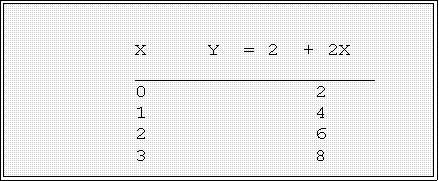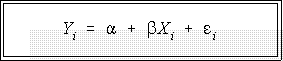REGRESSION ANALYSIS

1. AGENDA:
1. Correlation coefficient
2. Two variable regression analysis
3. Reading:
1. Correlation: Agresti and Finlay, Statistical Methods, Chapter 9, pages 318 to 323.
2. Regression: Agresti and Finlay, Statistical Methods, Chapter 9, pages 301 to 318



2. THE CORRELATION COEFFICIENT:
1. A the correlation coefficient, often called Pearson's r or the product-moment correlation, is perhaps the most commonly cited and used measure of linear association or correlation in the social and policy sciences.
2. Since we'll see a more formal definition in a moment, suffice it to say for now r is an index that tells how closely a the observations of a bivariate distribution--that is a simultaneous plot of X and Y as in the plots we have been working with--fall to a straight lone that does not have a zero slope.
1. A simpler way of saying this is that it measures how well a batch of X and Y data values "fit" a linear function.
3. Properties:
1. It is a "bounded" measure or index: its value lies between -1.0 and +1.0.
1. More formally:

1. For perfect positive correlation r = 1.0; for perfect negative correlation r = - 1.0
1. Alternatively one can say that the closer r is to 1.0, where the bars indicate absolute value, the closer the distribution is to a straight line.
2. A value of 0 indicates no linear correlation between X and Y.
3. Some pictures illustrate the point.
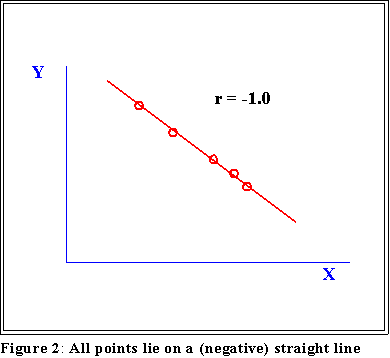
1. In the case of perfect positive correlation the value of r is 1.0

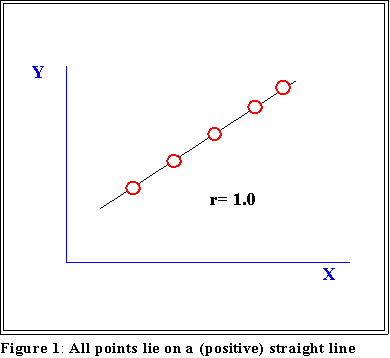
1. In the case of perfect negative correlation it is -1.0.

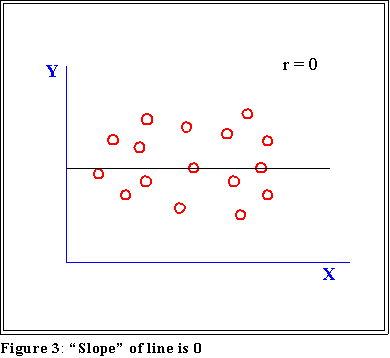
1. When there is no linear correlation r is 0.0
1. See next page

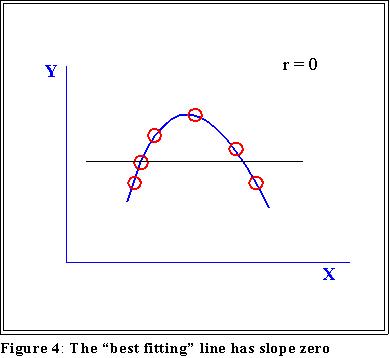
1. In this example, the data points are scattered randomly. The best fitting line has a slope of zero (see below).
1. Bur it is possible that r will equal zero even if the two variables, X and Y, have a "perfect" association, as in this example:

1. Most values of r lie between 0 and 1.0 or -1.0. The nearer the maximum value the "stronger" the linear correlation. For example:

:

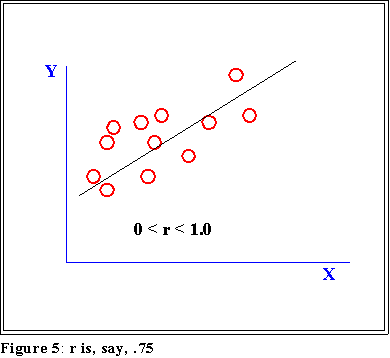
1. The points do not lie on a straight line, but they come "close" so the value of r is positive and, in this example, near 1.0, say .75.
1. See Agresti and Finlay page 321 for other examples.
2. Note also that if the data points slope down from the upper left to the lower right r will have a negative value.
3. The correlation coefficient is a scale free measure: its numerical value does not depend on the variables unit of measurement.
1. So for example, if one is examining the relationship between income and education, r will have the same value regardless if one uses dollars or yen or marks or pesos.
2. For this reason it is called a standardized measure.



1. TWO VARIABLE REGRESSION ANALYSIS:
1. Correlation is intimately tied to the notion of regression.
2. Regression analysis involves two questions:
1. Is there a mathematical relationship between X and Y?
2. If so, what is this relationship? How can it be described mathematically?
3. Some argue that a mathematical relationship expresses a social or political or economic "law" because it shows how one variable affects another.
1. It thus provides an explanation of the variation in a dependent variable.
4. A mathematical relationship also leads to prediction: if we know the value of X we can then predict the value of Y, subject to a certain amount of error if the relationship is not "perfect."
5. The mathematical relationship thus tells us in addition how much error or indeterminacy exists in the X-Y relationship.
6. A relationship of this sort can be expressed in several ways:
7. One way is:

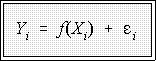
where Y_i is a value of Y_i, the dependent variable, f(x_i) means "is a function of X" and e_i represents a random error.

1. Ordinary regression assumes the function is linear or can be made linear.
1. Example a linear function or relationship:

1. Here the function is 2 plus 2 times X. The equation says, in effect, that scores on Y are produced (are a function of) by X. In particular, a Y score equals 2 plus 2 times a value of X plus an error. Thus if we know the value of X we could plug it into the formula and get a predicted score for Y. The error part is indicates that the function does not perfectly describe the dependent variable Y.
1. The goal of regression analysis is to estimate the function--to find the equation that links X to Y. One hopes that the error part will be as small as possible because the "data" will then nearly equal the "fit." Another way of saying this is that one wants to reduce the error so that the predicted values of Y will be as close to the observed values as possible.
2. What leads to a "good" fit?
1. An appropriate independent variable(s)
2. A correctly specified or estimated relationship



1. LINEAR MODELS:
1. Linear relationships
1. A useful mathematical relationship that "fits" a surprisingly large number of data sets is a linear equation between X and Y. It has the general form:

1. Interpretation:
1. a is the "intercept": it is the value of Y when X is 0
2. b is the "slope": the amount Y changes for a one-unit change in X.
1. The graph of the data point that fit a linear relationship is a straight line.
2. Geometry of a linear relationship
1. Example: consider these observed values for X and Y given the relationship--Y = a + bX.

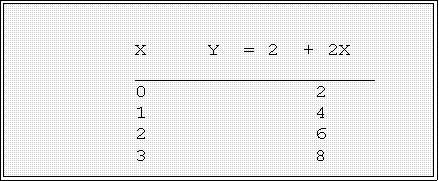
1. Here is the graph of these data:. Notice it is a straight line.
1. Here a = 2 and b = 0
2. As X increases by 1, Y increases by 2. When X = 0, Y = a = 2.

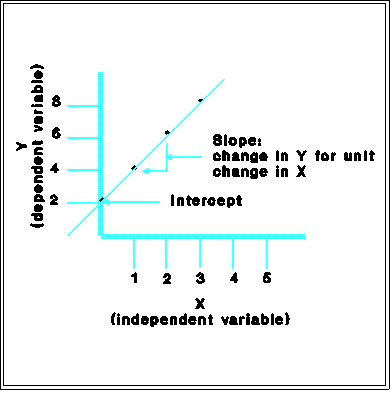
1. Interpretation: the graph of a linear relationship or function is a straight line with "slope" equal to b and "intercept" equal to a. If a set of data seem to fall on or near a straight line, one can infer that the variables are linearly related.



1. REGRESSION PARAMETERS:
1. The constants a and b are called regression coefficients.
1. In keeping with our standard notation we'll use Greek letters to denote population parameters.
2. b (b), usually considered the more important of the two, is called the regression coefficient.
1. It indicates the amount that Y changes for a unit change in X.
2. That is, assuming the linear model holds, if one could some increase X one unit, the numerical value of b would tell how much Y would change.
3. Suppose the regression coefficient equals 10. Then a one unit change in X "leads" to or is associated with a 10 unit change in Y.
4. If b equal -5, then changing X by one unit would decrease Y by 5 units.
5. Important: b or beta is measured in units of the dependent variable.
1. Suppose, for instance, we are regressing income (Y) measured in dollars on X, years of education.
2. If beta equals 4,000, we would conclude that a one year increase in schooling would produce $4,000 more income.
1. Note that we should write b = $4,000 since the unit of Y is dollars.
3. Another example: suppose we are examining the relationship between the poverty and crime rates. If Y is the number of violent crimes per 1,000 citizens and X is the poverty rate (percent individuals living below the poverty level) in counties then a regression coefficient of 2.7 would indicate that for every one percent increase in poverty we would expect the crime rate to go up by 2.7 crimes per 1,000 population.
4. Finally, if we were relating X, GNP per capita measured in tens of thousands of dollars, to illiteracy (measured as percent of the population that cannot read), a coefficient of -6.2 would mean that as a nation's GNP increases one unit (or $10,000 in this case) illiteracy would fall 6.2 percent.
5. Since b is measured in units of the dependent variable it is often difficult to compare regression coefficients for different variables.
3. a (a) is the regression constant. It indicates the value of Y when X equals zero.
1. Example: if a equals 100, then Y equals 100 when X equals zero.
2. In many instances the constant is of secondary importance in an analysis.
3. In fact, it sometimes doesn't make theoretical sense even if a regression program produces an estimate.
1. For example, suppose as above we are relating GNP to illiteracy. If a turns out to be 88.1, the literal interpretation is that if a country has no GNP (X = 0), we would expect its illiteracy rate to be 88.1 percent. But in this situation how meaningful is X = 0?
4. In the example of illiteracy and GNP the regression equation would be written:

1. LINEAR REGRESSION:
1. The two constants or parameters combined with the independent and independent variables and an error term define a linear regression function, which in our new notation is:

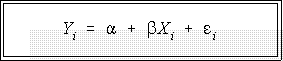
1. We'll consider this equation or function or model in more detail next time.
1. For now a another word about the correlation coefficient.



1. CORRELATION COEFFICIENT AGAIN:
1. The correlation coefficient is often used to evaluate the "fit" of a linear model to an observed batch of data.
2. Recalled that the total variation in Y is called the total sum of squares.
3. Recall in addition that this total can be broken into parts:
1. "Explained" by the independent variable, X, sum of squares and
2. "Unexplained" or error sum of squares.
4. Sums of squares are additive

1. One of the objectives of regression analysis is to estimate the explained sum of squares and what portion of the total it constitutes.
1. Another interpretation of r, the correlation coefficient:
1. r-squared: r², the second most commonly cited statistic, is often interpreted as the amount of variation in Y "explained" by X. The formula for r² is, loosely speaking:

1. r² is normally written with a capital, R²
1. r squared gives the portion of the total variation in explained by a regression model.
2. One might be tempted to think that r could be used to measure the "importance" of a variable in explaining some dependent variable.
1. After all, an X variable that has an R² = 80 suggests that 80 percent of the total variation in Y is explained or accounted for by X.
1. Although widely used for this purpose, it can be a misleading indicator and (in my view) should seldom if ever be used to measure the explanatory importance.
1. Example: debates about IQ frequently turn out to be duels between r's. Some investigators assert that a high value of R² (say, .45) between race and IQ shows that "nature" is a more important explanation of intelligence than "nurture" because the r between, say socio-economic status and IQ may be smaller (e.g., R² = .25).
2. This line of argumentation is often misleading if not down right fallacious, but it is very common.
1. NEXT TIME:
1. Further discussion of regression
1. More formal definition of the parameters.
2. Calculations
3. Numerous examples
4. Problems of interpretation

Go to Statistics main page

Go to H. T. Reynolds page.

Copyright © 1997 H. T. Reynolds