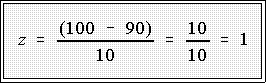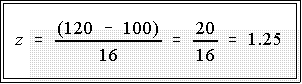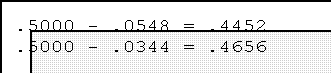DEPARTMENT OF POLITICAL SCIENCE

AND

INTERNATIONAL RELATIONS



Posc/Uapp 815



The Normal Distribution

(Continued)



  1. AGENDA:
    1. Using the normal distribution to solve problems.
      1. Areas under the normal curve
      2. Z scores
      3. Reading:
        1. Agresti and Finlay, Statistical Methods, Chapter 4, pages 86-99.


  2. QUESTION:
    1. Based on Agresti and Finlay's problem 4-19 (page 113).
      1. "The Mental Development Index (MDI) of the Bayley Scales of Infant Development is a standardized measure used in longitudinal follow-up of high risk infants. It has approximately a normal distribution with a mean of 100 and a standard deviation of 16."
        1. What proportion of children have MDI scores of at least 120?


  3. AREAS UNDER THE NORMAL CURVE:
    1. Before answering this question lets review briefly areas under the normal distribution.
    2. Area between one and minus one standard deviation.
      1. As we saw several times before, the area between 1.0 standard deviation is about 67%. Since the total area equals 1.0, the area above and below 1 standard deviation is 100% - 67% 34% (or in proportions 1.0 - .67 .34.)
        1. See the figure in previous notes
      2. Area between 2 standard deviations is about 95%, again as seen before.
      3. Area between 1.96 standard deviations.
        1. As seen in Figure 1 below the area between -1.96 and +1.96 standard deviations is 47.5% + 47.5% 95 percent.
        2. That means that about 5% of the area lies below -1.96 and +1.96 standard deviations.


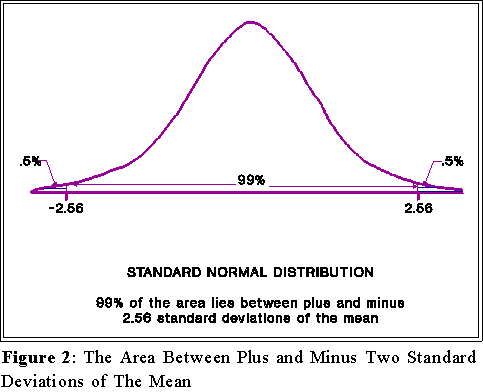
      1. Finally, the proportion of the area under the curve between 2.56 standard deviations of the mean is .99, as we have seen before and below in Figure 2.


    1. It's natural to ask how one "finds" the area under a normal curve.
      1. Note that although there a curve for every choice of and , they share common properties such as shape.
      2. Hence, if one knows the areas for one normal distributions, it's easy to find the corresponding areas in another.
      3. All that is necessary is to convert from one scale to another.
    2. The standard normal distribution.
      1. The areas under the curve of a normal distribution having mean = 0 and standard deviation = 1 has been extensively tabulated.
      2. Instead of calling the variable scale Y it is labeled z. So the standard normal distribution shows how values of z are related to f(z) and one can determine the area between any two points along the z scale by referring to a table.
        1. Computer programs (e.g., SPSS and MINITAB) compute the values directly, but we will use the table for most of our work.
      3. Moreover we can convert any Y score to a z score, which means that we can find areas between any two points Y1 and Y2 by converting them to z1 and z2 and looking in the table of the standard normal.




  1. STANDARDIZED OR Z SCORES:
    1. To use the standard normal distribution we have to change raw data to "standardized" data.
      1. Remember the standard normal distribution has a mean of 0 and a standard deviation of 1.0, but we usually deal with different measurement scales where, for example, the mean might be 500 and the standard deviation 25. Thus, we wouldn't know from the table how much of the area is in the interval from, say, 463 to 589.
      2. But we can find out by changing raw data to "standardized" or z scores.
    2. To convert the data follow these steps:
      1. Find the mean,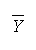, and standard deviation,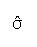of Y, the variable of interest.
      2. To convert a particular raw score to a standard or z-score use the formula:


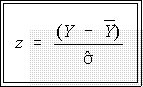
    1. z is called a standard value, a standardized value or a z score. They are all the same. z is obtained from the original data by subtracting the mean of the original data and dividing by the standard deviation.
    2. Examples:
      1. Suppose we have a batch of data with a mean of 90 and a standard deviation of 10. What is the z score corresponding to a raw score of 100?


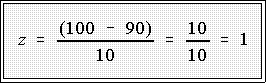
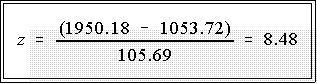
      1. Suppose now the data are such that the mean is 1053.72 and 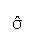is 105.69. What is the z score or standardized value corresponding to Y = 1950.18?

      1. z scores may be negative as this example illustrates: the mean equals 55.7 and the standard deviation,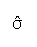, is 6.8. What is the z score for a raw value of 46.5?

      1. Finally, for the problem mentioned at the outset in which the mean is 100 and the standard deviation is 16 we need to find the z score that corresponds to 120.
        1. That's because we're going to see how much of the area lies above the point (i.e., z score) that corresponds with Y = 120.


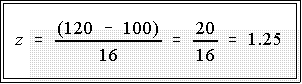
  1. THE STANDARD NORMAL TABLE:
    1. Now, find the area in the z-table that corresponds to the particular z. (Use a table of the standard normal distribution such as the one handed out in the last class.)
      1. Example: Find the row marked "1.2" and the column marked ".05."
      2. From the entry in the table we see that the area to the right of 1.25 is .1056.
        1. You can determine the meaning of the table entries by looking at the picture at the top. Most tables are organized in a similar fashion.
      3. Consequently, about 10.75 percent of the area of the standard normal distribution lies above z = 1.25. (How much lies below.)
      4. Moreover, given any normal distribution 10.75 percent of the area will lie above the score that corresponds to 1.25.
      5. Thus, in the present case in which the population mean is 100, the standard deviation is 16.0 and the scores are normally distributed, about 10 or 11 percent of the children will have MDI scores of 120 or higher.
        1. Note: the phrase is "scores of 120 or higher." .
      6. In a sample of 1,000 children we would expect to find about 1,000 X .1056 = 106 OR 107 of them above the 120 mark.


  2. MORE EXAMPLES:
    1. Suppose Y, IQ, is normally distributed with a mean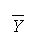= 100 and a standard deviation of 10. Find the probability--or if you prefer, the proportion of individuals in a batch--with IQs greater than or equal to 130?
      1. Convert 130 to a z score:

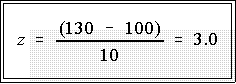
      1. Find the area in the z-table that corresponds to 3.0 (Use a table of the standard normal distribution.)
      2. As before, find the row marked "3.0" and the column marked ".00."
      3. The area to the right of 3.00 turns out to be .00135.
      4. Thus, if the mean of the population is 100, the standard deviation is 10.0 and the variable is normally distributed, less than 1% of a simple random sample (SRS) will have IQs of 130 or higher.
      5. In a sample of 100 people we would expect to find about 100 X .00135 = .135 persons or less than one person per 100 with an IQ greater than or equal to 130.
    1. Another example. If a normally distributed variable (say, an attitude scale) has a mean of 50 and a standard deviation of 3.5, what percent of the population would have scores of 58 or less?
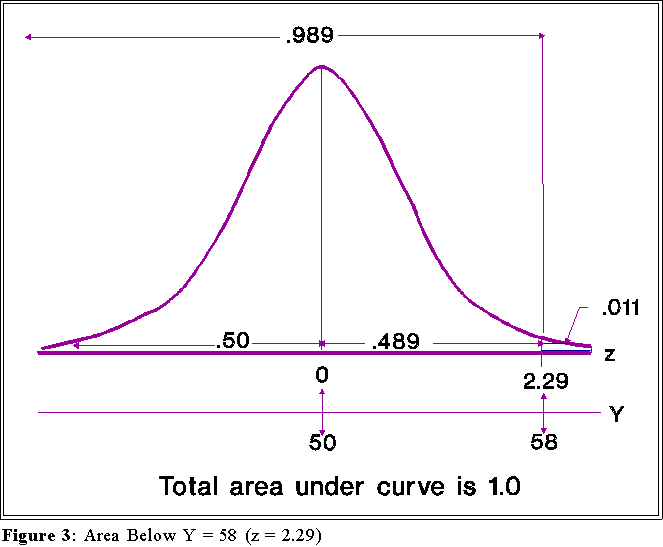
      1. Find the z score that corresponds to 58.

      1. Look in the standard normal table in the row marked "2.2" and the column ".09." The entry is .0110; this indicates that the proportion of the area lies above 2.29 and thus .5 - .0110 = .4890 of the distribution lies between 0 and 2.29 which is the same as saying 48.9% lie between 50 and 58 on the raw score scale.
      2. Taking into account the 50% lying in the lower half of the distribution (see below) that makes a total of 50 + 49.8 = 98.9% of the distribution which lies below 2.29 (or below 58). (See Figure 3.)

  1. FINDING SCORES THAT CORRESPOND TO AREAS:
    1. In many cases we will want to find a score that corresponds to an area.
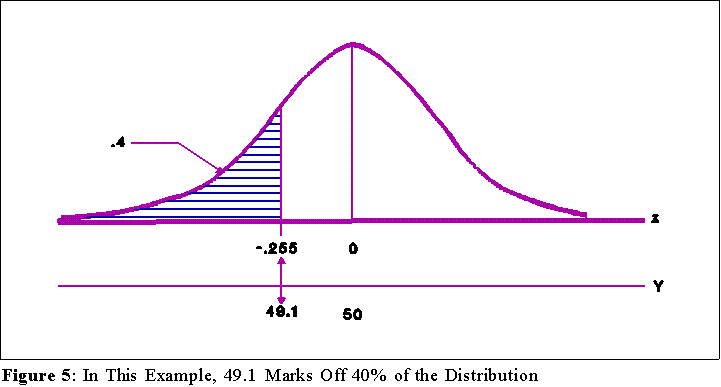
    2. Example: What is the raw score that corresponds to or defines the 40th percentile of a distribution with mean equal to 50 and standard deviation of 3.5?
      1. When in doubt draw a picture:

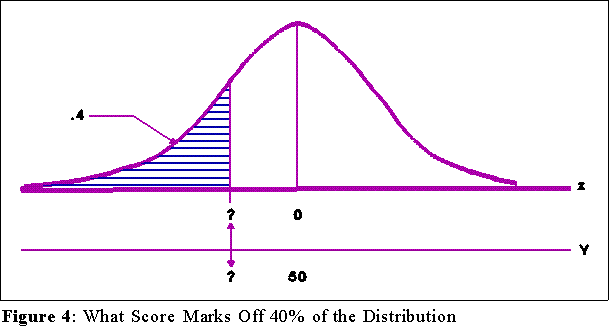
      1. Find the z score associated with .4000. This will be the point that defines the 40% of the area. From the table we see that it is about -.255. Remember: scores below the mean are negative. You have to add the minus sign.
      2. Now convert the z score to a raw score.
        1. Note that now we have to rearrange the formula

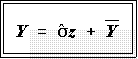
        1. After all, we know the z score and need the raw score that corresponds to it.
      1. In this example:

      1. Thus, 49.1 is the score that marks off the 40th percentile (see Figure 5, next page).




  1. ANOTHER PROBLEM:
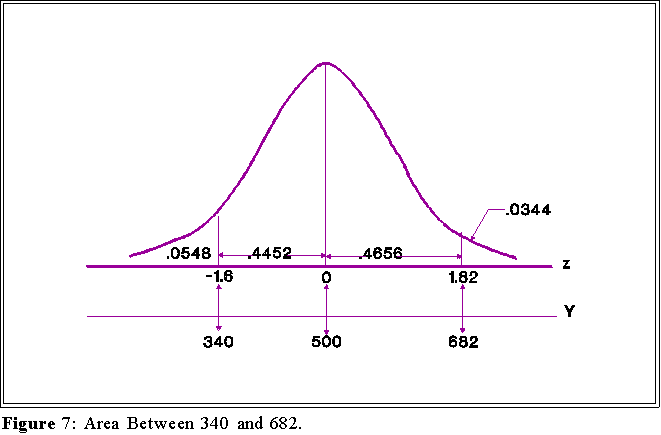
    1. The quantitative portion of a nationally administered achievement test is scaled so that the mean score is 500 and the standard deviation is 100. Assume the distribution is normal. What percent of students should score between 340 and 682?

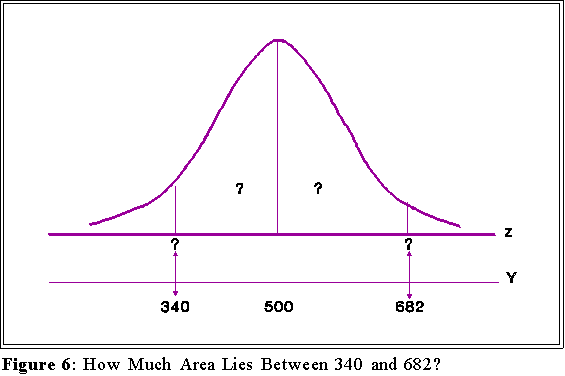
        2. Here we need to find two z scores as shown below (see Figure 6.)

      1. The two z scores are:

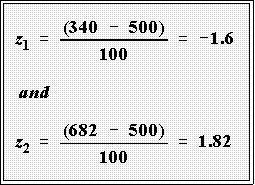
        1. Notice the minus sign in the first score. We have to look in the lower portion of the distribution to find it. (See Figure 4.)
        2. The areas associated with these scores are .0540 and .0344. To find the area lying between zero and these scores we have to subtract as shown in Figure 5.
        3. The areas between the mean and these two z scores are (look in the z-table), respectively:



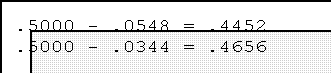
        1. Add them together to find the total percent or proportion lying between them: .4452 + .4656 = .9108.
        2. Thus, about 91.08 percent of the scores lie between 340 and 682 which means that about 100 - 91.08 = 8.78 are either above or below these scores.
          1. See Figure 7 below.


  1. NEXT TIME:
    1. The standard normal distribution underlies hypothesis testing so we will explore it in more detail.
    2. Tests for normality
      1. Does an observed variable "fit" a normal distribution?

Go to Statistics main page

Go to H. T. Reynolds page.

Copyright © 1997 H. T. Reynolds