Light Propagation in a Dielectric

        The propagation of light through chemical materials is described by a wave equation similar to the one that describes light travel in a vacuum (free space).  Again, using E as the electric field of light, v as the speed of light in a material and z as its direction of propagation.

                

.

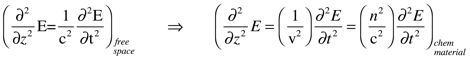
(Reads: the variation in the electric field with respect distance traveled is proportional to its variation with respect to time.) The refractive index, n, describes how matter affects light speed: through the electric permittivity, ε, and the magnetic permeability, μ.

                                                           

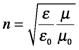
These properties describe how well a medium supports (permits the transmission of) electric and magnetic fields, respectively.  The terms ε0 and μ0 are reference values: the permittivity and permeability of free space.  Consequently, the refractive index for a vacuum is unity.  In chemical materials, ε is always larger than ε0, reflecting the interaction of the electric field of the incident beam with the electrons of the material.  During this interaction, the energy from the electric field is transiently stored in the medium as the electrons in the material are temporarily aligned with the field.  This phenomenon is referred to as polarization, P, in the sense that the charges of the medium are temporarily separated.  (This must not be confused with the polarization that refers to the orientation or behavior of the electric field.)  This stored energy is re-radiated, but the beam travel is slowed by the interaction with the material. So, as the wave equation above shows, the refractive index also is the ratio of the speed of light in a vacuum, c, to the speed of light in the material, v.

                                                               

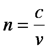
Energy in the beam is conserved as long as absorbance by the material is negligible.

        The wave equation states that the derivatives of light amplitude with respect to time and distance are proportional, related through the velocity.  The only functions that satisfy this criterion are oscillations in time and space:

                    

.

However, in this case, the wavevector k is ω/v= ω/(c/n)=2π(λ/n), where c/n is the speed of light in the material.

        For all chemical materials, n is larger than 1 at all but X-ray wavelengths due to the interaction of the material electrons and incident electric field.  A material that has ε≠ε0 and negligible magnetic interactions, i.e., μ=μ0, is called a dielectric material.  Materials that have tightly bound electrons, such as glasses and other optical materials, are dielectrics. However, it can be more convenient to use the electric susceptibility, χ, rather than the refractive index to describe interactions of light with these materials because χ is zero in a vacuum, making it more directly related to the extent of the physical interaction of light and the material.

                                                            

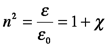
The electric susceptibility measures the ability of a material to become transiently polarized, and the amount of polarization is proportional to χ and the electric field strength:

                                                        

.

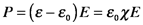
This relation holds as long as the electrons oscillate at the same frequency as the electric field, i.e., as long as the intensity of the electric field is relatively low.  In nonlinear materials, i.e. those that have specific types of structural anisotropies, intense laser beams (large electric fields) induce oscillations that have other frequency components.  (More on this later.)

        For chemists, the polarizability, α, is more familiar than the electric susceptibility, χ.  (Remember the discussion of the electrophilic addition of iodine vs bromine in Organic? If not, ask.) The polarizability is linearly related to the electric susceptibility:

                                                                  

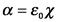
The refractive index is thus a measure of the polarizability of the material.

                                                               

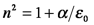
One of the important features of these parameters (that is not evident in the wave equations) is that they are frequency (and wavelength) dependent.  To see this, we analyze the electric susceptibility by describing the chemical material as through it were a collection of N electrons bound to N atomic nuclei per volume.  Since these charges are bound, they have a natural resonant frequency, designated as ω0 (remember from PChem?).  Assuming a linear response to incident electric fields, and that oscillations fade with time after their source is turned off, the system acts as a damped harmonic oscillator.  Solving this system (as you will for homework) reveals that χ is given by

                                                      

.

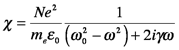
In this expression, the charge of an electron is e, the mass of the electron is me and the damping coefficient is γ, which is the inverse of the lifetime of the oscillator.  The consequence of this physics is that the electric susceptibility consists of two components.  χ is a complex quantity because photon irradiation induces two independent physical responses in the material: dispersion (the wavelength dependent propagation of the beam through the material) and absorption (the wavelength dependent transfer of energy to the interior structure of the material).  Since the refractive index is a function of χ, it must also be a complex quantity: n = nreal+inimag.

                                                   

Plots of the real and imaginary parts of n as functions of frequency are shown in Fig. 3A.  The real part of the refractive index, nreal, is what we normally call the refractive index; tabulated values of

the refractive index (often measured at 589 nm) refer to nreal. Far from resonance, nreal is a weak function of frequency, i.e., it does not change much.  In the vicinity of the resonance frequency, the refractive index behaves strangely: nreal first increases quickly, then falls below unity, and eventually makes its way back up toward unity. This behavior near resonance is called anomalous dispersion.  The imaginary part of the refractive index, nimag, is a very weak function of frequency far from resonance.  Near the resonance, the imaginary refractive index increases sharply to a maximum then falls as the frequency exceeds the resonance frequency.  The shapes of these functions for nreal and nimag will eventually be familiar if they aren’t already. The real part of the refractive index matches the imaginary part of the generic solution, which is called a dispersion function:

               

.

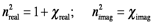
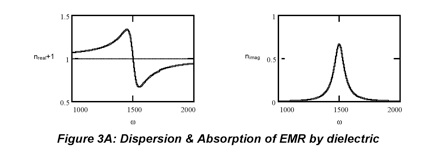
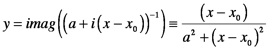
The imaginary part of the refractive index has the same shape as the real part of the generic solution which is a Lorentzian function:

             

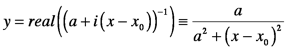
Lorentzians are distinguished by the fact that their bandwidth is 2a.  In spectroscopy, the focus is resonances so, nimag is large but changes in nreal with frequency are typically small enough to be ignored in the experimental design. For example, the absorptivity of a typical dye is so high that a solution can be very darkly colored yet its refractive index rarely exceeds 2.  In optics, on the other hand, the radiation is off-resonance so, nimag is negligible while nreal is used to control beam direction through refraction (next Section).

        A convenient alternative notation for the solution of the wave equation describing light propagating in materials is complex notation using Euler’s relation: eiθ=cosθ+isinθ.

                                                       

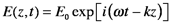
We could avoid imaginary numbers by using E(z,t)=(1/2)E0{exp[i(ωt-kz)]+ exp[-i(ωt-kz)]}, which is the same as E(z,t)=E0cos(ωt-kz).  However, derivatives of trigonometric functions are much more cumbersome than those of exponents.  Besides, complex quantities are efficient for describing processes that are related but distinct.  The variable definitions are the same as listed in the first Section (Nature of Light).  By substituting k=ω/(c/n), the electric field is separated into two components.  The first is phase-shifted compared to the incident radiation in free space and the second is attenuated:

         

.

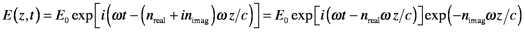
This equation states that light in a medium of refractive index n oscillates at frequency ω, but experiences a change in apparent velocity to v=c/n.  The change in velocity (and wavelength) can also be viewed as a phase-shift in space by (nreal -1)z/c compared to the same beam traveling in a vacuum.  This equation also shows that the electric field amplitude exponentially decays as it travels in the direction z by an amount that depends upon nimag.

        Since detection encodes the electric field as the irradiance:

                                                           

,

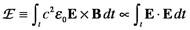
substituting the EMR expression above into the irradiance integral yields

                                                           

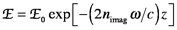
This relates to something very familiar. Remember Beer's law, which states that -log(T) = εbC, where T= E/E0.  (Remember this ε is not permittivity.)  If the path length, b, is made to be a variable, i.e., b=z, and we convert from base 10 to base e, then Beer’s law states E/E0= exp(-2.3εzC).  Consequently, nimag is directly related to the molar absorptivity.

        There are circumstances in which the polarization deviates from the simple proportionality to E described above. Intense beams propagating in non-linear optics induce polarization that is approximated by a series expansion that includes first order, second order, etc., electric susceptibilities.  The sizes of the higher order susceptibilities are much smaller.

                                                           

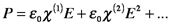
What we have been calling the electric susceptibility is now represented by χ(1) and the higher-order nonlinear susceptibilities are χ(n).  (Note that this is not a power, i.e., χ(2) is not χ2.)  In the wave equation, the refractive index, n, now includes the higher order susceptibilities, which changes the solution to the wave equation.  As an illustration, if the χ(2) term is significant, while χ(3) and the higher terms are negligible, the wave equation (in one direction) becomes the following:

                                                     

.

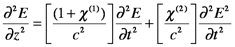
The E2 term describes an oscillation at 2ω, twice the frequency of E (You can demonstrate this using trigonometric identities for sin2θ and cos2θ, etc).  The result is that frequency-doubled light is generated.  In practice, frequency doubling is very valuable.  It is commonly used to convert IR beams to visible, for example, to convert the 1064 nm Nd:YAG laser beam to 532 nm.  Crystals that have large second-order susceptibilities, e.g. potassium dihydrogen phosphate (KDP) and lithium niobate (LiNbO3), are used, and the incoming laser beam is tightly focused to maximize E.  Second harmonic generation (SHG) increases with the coherence length, lc, of the material, which is given by

                                                                 

,

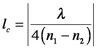
where n1 and n2 are the refractive indices of the material for the fundamental (ω) and doubled (2ω) frequency, respectively.  The efficiency of SHG is given by

                                                   

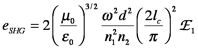
where μ0 and ε0 are the permeability and permittivity of free space, respectively.  The non-linear optical coefficient of the material, d, is related to the second order susceptibility, (2).  E1 is the irradiance of the fundamental beam on the crystal.  There has been a considerable effort in materials science to create thin films having large values of χ(2) (or d) because such a material could be used in optical computing. One red light beam of E1 would switch another red light beam of E2 because the output would be the product E1E2 with a frequency in the UV.  Optical switching would greatly increase the speed of computing for scientific calculations and searching of databases, as well as telecommunications to enable much faster graphical communications such as faster access to the files on the world wide web and broad use of video telephones.  There also has been phenomenal growth in the development and application of nonlinear spectroscopies that usually involve the interaction of more than one laser beam with the analyte.  Examples of nonlinear spectroscopies include multiphoton absorption, nonlinear Raman scattering, harmonic and sum-frequency generation.  Many of these techniques have important advantages relative to linear spectroscopies.  For example, second harmonic and sum-frequency generation measurements are surface specific.

(3.2)

(3.3)

(3.4)

(3.5)

(3.6)

(3.7)

(3.8)

(3.9)

(3.10)

(3.1)

(3.11)

(3.12)

(3.13)

(3.14)

(3.15)

(3.16)

(3.17)

(3.18)

(3.19)

(3.20)