| Last revised 1999/10/26 |
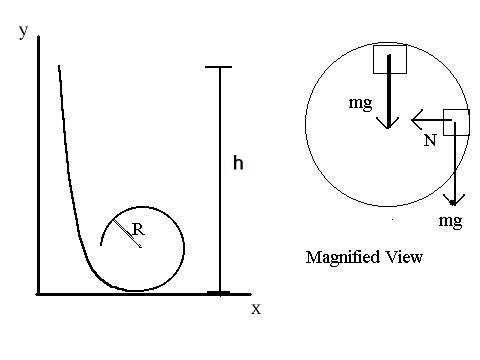
Further example: HRW pp. 176-185 # 45.
10 & 39

40.
(From a MATHCAD file.)




45.
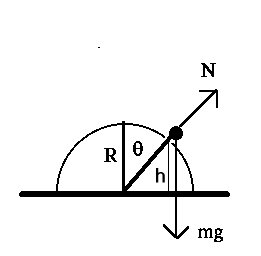
This problem is very much like the loop-the-loop (#10 and 39). The
boy is held in circular motion by the combination of the normal force
and the radial component of mg. The required normal force gets
smaller and smaller as he slides down the hemisphere. He cannot
remain in circular motion if the required normal force is inward; thus
the last point he will be in circular motion is where N=0. We will
therefore be using the formula for centripetal acceleration with F=ma.
To get the boy's velocity, which we need in orderto determine his
centripetal acceleration, we will have to use energy conservation. It
will prove convenient to place the zero of gravitational potential
energy at the base of the semicircle; the height of the boy is then
h=R cos(theta).
The necessary relations are:
mg cos(theta) - N = m v2 / R
[with N=0]
(1/2) m v2 + m g R cos(theta) = const.
h = R cos (theta)
At the top of the semicircle, v=0 and theta=0, which allow us to write
0 + m g R = (1/2) m v2 + m g R cos(theta)
for the second equation (energy conservation). The first equation (circular motion) is
mg cos(theta) = m v2 / R
which gives
v2 = g R cos (theta)
Putting this value for v into the equation for circular motion gives
m g R = (1/2) m g R cos (theta) + m g R cos(theta)
which may be solved to give
cos (theta) = 2/3
Then substituting cos (theta) into the formula above for the height
h = R cos(theta)
= (2/3) R
44
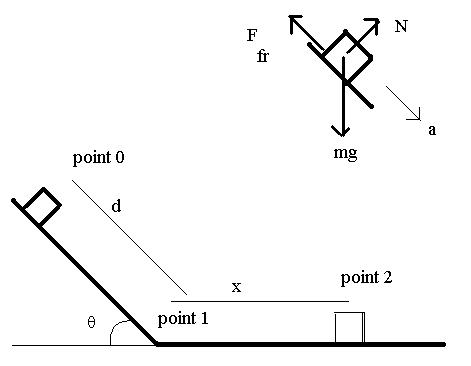
Ugr = m g x sin(theta)
Usp = (1/2)K x2 for x < 0
= 0 for x > 0
The reference point for the potential energy of the spring must be at x = 0, so to avoid confusion we should place the reference point for gravity there as well. In that case, energy conservation reads
0 + 0 + m g d sin(theta) = (1/2)m v2 + (1/2) K x2 + m g x sin(theta)
since x = d in the initial position.
(a) In the first part, we are to find the initial distance up the plane given the point of maximum compression of the spring. At the point of maximum compression, v = 0, and x = xf < 0, so
m g d sin(theta) = (1/2) K xf2 + m g xf sin(theta)
d = [(1/2) K x2 + m g xf sin(theta) ] / [m g sin(theta)] = 0.40 m
Remember that xf is negative.
(b) In the second part, we are to find the point at which the block has the highest speed. Energy conservation for this point is
m g d sin(theta) = (1/2)m v2 + (1/2) K x2 + m g x sin(theta)
Solving for v2 gives
v2 = 2 g d sin(theta) - (1/2) K x2 - m g x sin(theta)
We want the position of the largest value of v, which is the same as the position of the largest value of v2 . Since we can adjust x, we find the location of the maximum by differentiating with respect to x and setting the result equal to 0:
0 = d (v2) / dx
= - K x - m g sin(theta)
x2 = - (m g / K) sin(theta) = - 0.04 m
which is negative, as it must be.
46.
(From a MATHCAD file.)
49.
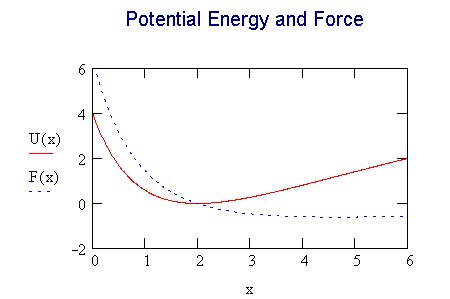
Use the text's figure 8-50 to understand these answers:
(a) If the system has a total energy of 1.0 on the diagram, the atoms can be any distance apart greater than about 0.08 nm. About the only way that they can get close is for them to approach each other from a long way away (right side of the diagram), get to 0.08 nm away where the KE vanishes => the velocity vanishes. Here they turn around and go back away from each other, continuing as long as you wish to keep track. This behavior is called "having a turning point at 0.08 nm."
(b) If the energy of the system is E2, the kinetic energy is positive and therefore the relative velocity real only between 0.15 nm and 0.3 nm. Since the relative velocity must be real, the system can only exist with an energy of E2 if the distance between the two atoms is between 0.15 and 0.3 nm.
(c) Reading from the graph, the potential energy of the system at r = 0.3 nm is approximately -1 x 10 -19 joules [the position of the orange curve].
(d) The total kinetic energy of the system at that point is the difference between the total energy E1 = 10 -19 joules and the potential energy of about -1 x 10 -19 joules, which is 2 x 10- 19 joules.
(e) The slope of the potential-energy curve at r = 0.3 nm is about + 1 x 10 -19 joules/ (10 -10 m ), so the force on each mass is about 10 -9 Newtons. For each mass the force points toward the other mass.
(f) The force is repulsive where the slope of the potential-energy curve is negative, which is from at or just outside 0 to just beyond 0.2
(g) The force is attractive where the slope of the potential-energy curve is positive, which from just beyond 0.2 to the end of the plotted curve.
(h) The force is zero where the potential-energy curve is at an extremum, which is at a point just beyond 0.2 .
75.
(From a MATHCAD file.)







Links to image files used in these solutions:40, 40a, 40b, 40c, 49d,45, 46a, 46b, 75, 75a, 75b, 75c, 75d, 75e, 75f, 75g. |