| Last revised 1999/09/30 |
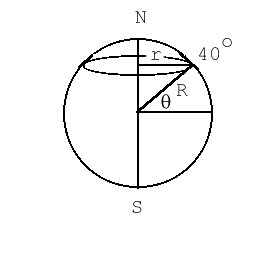
N and S mark the north and south poles, respectively.
Theta is, of course, necessarily 40 degrees.
r is the distance from a point on the 40-degree
latitude circle to the rotation axis of the earth.
| Radius of the earth (see table on front cover of text) | R = 6.37 x 106 m |
| Theta | Theta = 40 x pi / 180 |
| Radius of latitude circle | r = R sin(theta) |
| Circumference of latitude circle | c = 2 pi r [r, not R] |
| Velocity of person on latitude circle | v = unknown and unwanted |
| Acceleration of person on latitude circle | a = wanted |
The person is being carried around a circle by the rotation of the earth. Hence we need to analyze the centripetal acceleration in circular motion. To do this we need the speed, which is given by the distance travelled divided by the time [definition of speed]. But the distance travelled is once around the circle per day. So
a = v2 / r
r = R cos(theta)
v = 2 pi r / (1 day)
Hence after some algebra a = 4 pi2 R cos(theta) / (1 day)2
a = 0.03 m / sec2 compared to g = 9.8 m / sec2 ; reasonable in size.
By symmetry, Galaxy A sees us moving away at a speed of - v. However, the speed of Galaxy B is an addition of velocity problem and obeys the relation from section 4-10:
v' = (v1 + v2 ) / (1 + v1 v2 / c2 )
with c=3.00 x 108 m/sec. Since in this case v1 = 0.35 c and v2 = 0.35 c we have
v' = ( 0.35 c + 0.35 c) / (1 + (0.35 c)2 / c2 )
v' / c = 0.62 c
not 0.70 .
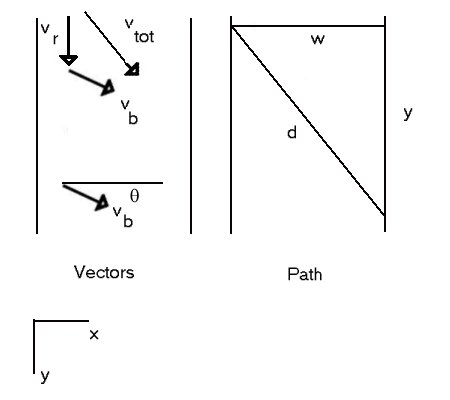
| Velocity of water in river | vr , known |
| Magnitude of velocity of boat relative to water | vb , known |
| Rowing angle | theta, needed |
| Velocity of boat relative to bank | vtot |
| Time of travel in river | t1 Same as T in problem IV |
| Total distance travelled | d |
| Width of river | w = dx , known |
| Distance down the river | y = dy , needed |
| Walking speed | vw , known |
| Time spent walking back upstream | t2 |
| Total time for trip | ttot , requested |
t1 = w / [vb cos (theta)]
y = w [vr + vb sin (theta) ] / [vb cos (theta) ]
To get the time required to walk back to the point opposite the starting point, we simply have to use the walking speed. We have to be careful about signs, but in IV y was defined to be positive, so
t2 = w { [vr + vb sin (theta) ] / [vb cos (theta) ] } / vw
We add these two to get the total travel time. Then we must adjust theta to get the best travel time, which is done by using the calculus relation d (ttot) / d theta = 0. However, if the differentiation gives us a negative value of t2 , the result is meaningless. We can't get time back by walking downstream! So if d (ttot) / d theta = 0 gives an angle which makes t2 < 0 , we must require t2 = 0 instead. From the equation for t2 above, we can see that t2 = 0 requires sin(theta) = - vr / vb. Any value of theta more negative than this must be rejected.
ttot = w / [vb cos (theta)] + w { [vr + vb sin (theta) ] / [vb cos (theta) ] } / vw
ttot = { w / (vw vb cos(theta) } { vw + [vr + vb sin (theta) ] }
d ttot / d theta = { w / (vw vb } { - sin (theta) (vw + vr ) - vb } / cos2 (theta) = 0
Solving,
sin(theta)(vw + vr ) + vb = 0
sin(theta) = - vb / ( vw + vr), a value that implies rowing upstream, as expected.
This result and the value of ttot above, solve the problem. There is no advantage that I can see of substituting the optimized value of sin(theta) into ttot .
Since the tangential component of the velocity has magnitude dL/dt , where L is the distance travelled along the circle, we can treat the tangential motion as one-dimensional motion with constant acceleration and find the centripetal acceleration at any given time from the tangential velocity at that time. Hence the equations are
| vt = 0 + at t | L = 0 + 0 t + at t2 / 2 |
| ac = vt2 / R | |
with known values being
| at = b = pi/2 m/s2 | vt = ? |
| R = 1 m | ac = ? |
| Lf = pi R | t = ? |
Then
Lf = n pi R = b t2 / 2 , with n=1 in this case, gives
(a)
| t = sqrt (2 pi R / b ) |
At that point, vt = at t or
(b), (c)
| vt = b sqrt (2 pi R / b ) down |
and from the expression for ac above
(d1)
| ac = 2 pi b |
(d2) and the tangential acceleration is at = b .
(e)
atot = ac + at
so
| a | = b ( 1 + pi2 )
tan (thetaa) = pi + [ 1 / (2 pi) ]
Using w to mean omega.
It really is easier to see what is going on if we use symbols rather than numbers. Therefore let us write the position as
r = x0 sin wt 1x + y0 cos wt 1y
where in this problem x0 <> y0
(a)
This equation is the equation for an ellipse.
We now differentiate this equation once to get v and then again to get a. First
(b)
v = wx0 cos wt 1x - wy0 sin wt 1y
For future reference, we note that v2 = | vx |2 + | vy |2 = w2 x02 cos2 wt + w2 y02 sin2 wt
(c)
Then, with a second differentiation,
a = -w2 [x0 sin wt 1x + y0 cos wt 1y] = - w2 r
which is, of course, in the direction of (-)r
(d)
Next we want to find the places where the speed (the magnitude of the velocity) is a maximum or a minimum. The |v| will be a maximum or a minimum at whatever time v2 is, so we can differentiate v2 instead of |v| to find the locations. It is usually true that v2 is easier to differentiate than |v|. Using the expression for v2 from above:
0 = dv2 / dt = - 2 w3 x02 sin wt cos wt + 2 w3 y02 sin wt cos wt
= 2 w3 sin wt cos wt (y02 - x02 )
which implies t = 0 , pi/(2w), pi/w , 3 pi / (2w), ... for the times when the velocity is maximum or minimum. These times are when the particle has one of x = 0 or y = 0 .