| Last revised 1999/09/20 |

| First average speed (either case) | v1 = 35 mi/hr |
|---|---|
| Second average speed (either case) | v2 = 55 mi/hr |
| Overall average speed (either case) | vave = ? |
| Time of first part of trip (either case) | t1 |
| Time of second part of trip (either case) | t2 |
| Total time of trip (one way: either case) | T |
| Length of trip | L |
| Average velocity for round trip | V |
| Part (a) | Part (b) |
|---|---|
|
D = vave T
D = v1 T/2 + v2 T/2 |
D = vave T
D = v1 t1 + v2 t2 D/2 = v1 t1 D/2 = v2 t2 T = t1 + t2 |
| Solving A1 and B1 for the velocities we want: | |
| vave = D / T Substitute for D from A2
vave = (1/T) [ (v1+ v2 ) T/2 ] |
vave = D / T Find t1 and t2 from (B3) and substitute into (B4) T = D / (2 v1 ) + D / (2 v2 ) so that
vave = D / [D / (2 v1 ) + D / (2 v2 )] |
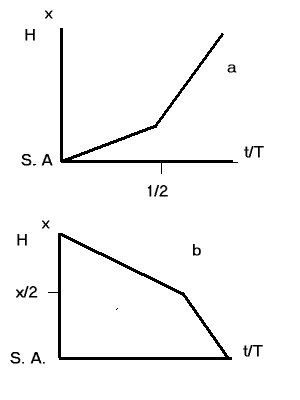
The two averages are not the same. The average volocity for physics is a time average (switching at the halfway time), not a spatial average (switching at the halfway distance). Therefore the physical average corresponds to the average found in part (a).
Part (c)
The average speed for the round trip is another case of averaging one speed for half the distance of a trip and another speed for the other half. Thus the method of part (a) applies, and
Vave = [ 1/(2 va) + (1/(2 vb)]-1
Vave = 43.9 mi/hr
Part (d)
The average velocity for the trip is v = (r1 + r2)/T, but r1 = - r2, so the (vector) velocity is zero.
Part (e)
The requested graph is the upper one in the figure at the beginning of the solution. The slope of the line connecting the beginning of the trip (t=0) with the end of the trip (t=T) is the average speed.
| Speed of each train: | vt = 30 km/hr |
|---|---|
| Speed of bird: | vb = 60 km/hr |
| Initial distance between trains: | d0 = 60 km |
| Distance travelled by bird: | D = ? |
| Number of trips by bird: | N = ? |
| time before trains meet: | T |
We know the bird's speed, so if we knew how long it flew we would know how far it went. But it flies until the trains reach the same place at the same time. Since we know how fast the trains come together and how far apart they were at the beginning, we can calculate the time it takes the trains to come together.
d = 0 = d0 - (2 vt) T [from trains' motion]
So T = d0 / (2 vt )
Then substituting for T in the equation for the bird's motion
D = vb [ d0 / ( 2 vt) ]
D = 60 km.
2 < t < 3: In this region, x < 0 so the armadillo is left of the origin on the x-axis. Also, x is still decreasing and the animal's velocity is negative. At t = 3 the slope of the tangent to x(t) vanishes. Hence at that time the animal's velocity is zero.
3 < t < 4: Here x < 0 and the armadillo is still left of the origin. The slope of x(t) is positive and x is increasing, so the animal's velocity is positive. At t = 4 the animal reaches the origin.
4 < t: Here x > 0 and v > 0. The armadillo is to the right of the roigin and moving further to the right.
The acceleration is positive everywhere the line is curved
upwards.
The acceleration vanishes everywhere the line is straight.
The acceleration is negaive everywhere the line is curved downwards.
(b)
Just to the left of B the line is curved downward and you know that
the acceleration is negative. Just to the right of B the line is
straight and you know that the acceleration vanishes. Somewhere
between these two regions the acceleration had to change, but you
can't tell by simple visual inspection exactly where the change took
place or how long the acceleration was not constant.
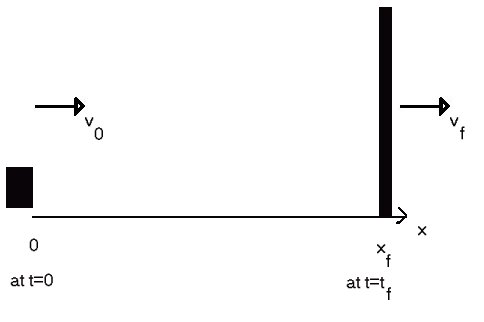
| Starting speed of automobile | v0 = 56 km/hr |
| Initial distance of barrier from automobile | d = 24.0 m |
| Time elapsed before hitting harrier | t = 2.00 s |
| Acceleration of car | a = ? |
| Speed of car at impact | vf = ? |
x = x0 + v0 t + (1/2) a t2
v = v0 t + a t
where t is the time interval between the measurement of x and the determination of x0 and t0 . It is convenient in this problem to put the origin of both x and t at the initial position of the car. Then x0 vanishes, and the final position is the position d of the barrier.
d = 0 + v0 t + (1/2) a t2
in which only a is unknown. Hence
a = 2 (d - v0 t) / t2 = -4.61 x 104 km/hr2
If we substitute this value for a into the second equation, we get the final velocity vf directly:
vf = v0 + [ 2 (d - v0 t) / t2 ] t
vf = - v0 + (2 d)/t = 30.4 km/hr
Hopefully the driver was wearing a seat belt.
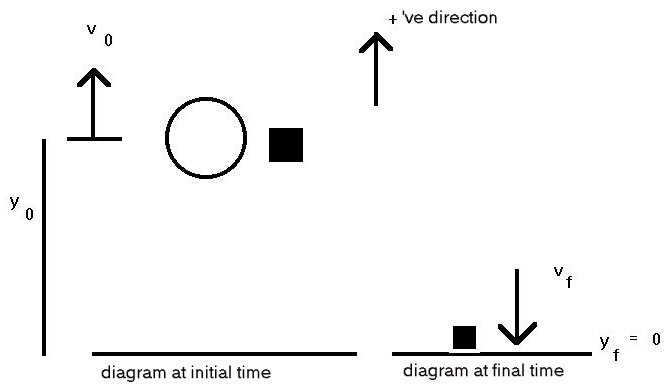
| Speed of balloon: | v0 = 12 m/sec |
| Height when package is dropped: | y0 = 80 m |
| Time required to reach the ground: | delta t = ? |
| Speed of package at ground: | vf = ? |
| Final position of package: | y = 0 m |
| Acceleration of gravity: | g = 9.8 m/sec2 |
v = v0 + a (delta t)
| 0 = y0 + v0 (delta t) - (1/2) g (delta t)2. | (1) | [only the time inverval is unknown] |
| v = v0 - g (delta t) | (2) | [the final speed and the time interval are unknown] |
Solve (1) for the time interval, and then (2) will give the final speed. Since (1) is quadratic, we get two possible answers:
| delta-t1 = [1/g] [v0 + sqrt(v02 + 2 g y0) ] = 5.45 sec |
| delta-t2 = [1/g] [v0 - sqrt(v02 + 2 g y0) ] = - 3.00 sec |
The second time is before the package is released. This value is impossible and can be rejected as an unphysical solution [it actually is the time at which the package would have to be thrown upward from the ground in order to reach the balloon at t = 0]. Therefore time interval between our dropping the package and its hitting the ground is 5.45 sec.
The value delta-t2 may be substituted into equation (2) to give
v = - sqrt( v02 + 2 g y0) = -41.4 m/sec2 .
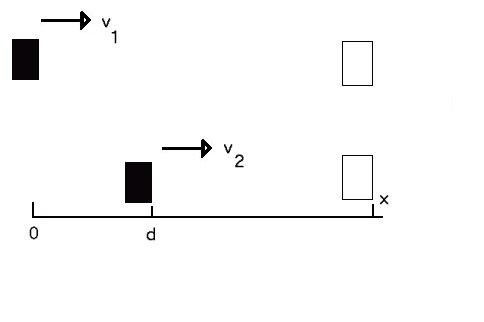
The solid rectangles show the positions of the two cars at t = 0 and the outlined squares show their positions at t = tf .
x1 = 0 + v1 t
x2 = d + v2 t
x1(tf) = x2(f)
The initial positions in the first two equations are chosen, looking at the diagram, to represent the distance between the two cars at t = 0. The third equation is the condition that they be side by side at t = tf
v1 tf = d + v2 tf
so that
tf = d / (v1 - v2 )
which gives the answer to the question of "when." Substituting into the equation for x1 gives
x1 = x2 = d [v1 / (v1 - v2 )]
which tells us where they are beside each other.