Ion Velocity Fourier Transform Mass Spectrometry
Eugene Nikolaev, Sergey Rakov and Jean Futrell
Introduction
A new concept is proposed for mass spectrometry based on Fourier transform analysis of
the detected image current generated by ions with a certain velocity ensemble. The induced
charge density function developed by a single ion traveling in an infinitely long tube electrode is
derived. Electrostatic ion beam guide designs for linear and cyclic-orbit trajectory mass analyzers
are proposed. Computer simulations using MATLAB 4.2 and SIMION 6.0 interfaces were
performed to support the proposed designs in terms of field distribution and ion trajectory
dynamics.
The idea of using an induced charge as a signal source for FT analysis has been used
routinely in Fourier Transform Ion Cyclotron Resonance. Conventional FT ICR cells use two
detection electrodes systems. Orbiting charged particles induce the current between the two
detection plates. The current undergoes Fourier transformation and is presented in the form of the
mass spectrum. Systems with more then one pair of detectors have also been studied, [1],[2].
We designed and studied a detector which implements the idea of periodic induced current
detection for mass analysis without the drawbacks of requiring high magnetic fields. Here we
present four possible geometries for the FTIV MS which adequately illustrate the concept and
applications: (1) the field free linear periodic ring detector array, (2) the stacked lens ion guide,
(3) spherical ion trap periodic detector array [3], and (4) cylindrical ion trap periodic detector
array. They are discussed it terms of induced current function, beam packet dissipation and the
resulting resolution restrictions. Computer simulations are provided where necessary. Although
these four examples are not the only geometry designs suitable for the implementation of the
technique, they adequately illustrate the possibilities and advantages of FT IV MS.
General Approach
In all the cases we pose the same initial conditions-, namely, we start with a point source
of monochromatic ions with a given angular divergence at the entrance of the detecting array. For
each detector geometry we calculate the potential distribution along the beam path. In most
geometries we can analytically calculate the ion trajectories. Simultaneously the induced charge as
a function of ion position inside the detector is derived. Summation for all the electrodes inside
the same group follows. Combining these results we obtain an induced charge density function as
a function of time. Taking its time derivative we get the induced current. As we expand it in
Fourier series we immediately obtain the frequency spectrum, which is finally transformed in the
mass spectrum.
Next we examine the phase divergence of the beam (natural broadening of the spectral
lines) for this particular design of ion guide and consider how to decrease it. Careful derivation of
aberration coefficients and computer simulations are important at this stage of analysis. Prediction
of resolving power is then obtained as a convolution of broadening and ideal resolution. There
are several general sources of broadening of an initially monochromatic beam:
- initial angular divergence of an incoming ion beam,
- finite incoming beam cross-section,
- field gradient tangential to the centroid-trajectory,
- finite acquisition time,
- and odd harmonics generation introduced by essentially non-central
trajectories, [1]
Aberrational properties which cause the broadening for each of the ion guides considered are
typical for a given geometry.
Realization and Resolution Predictions
The simplest way to implement this concept is to construct a periodic linear array of
detecting plates or rings which will generate the required ion velocity
signal is shown below:
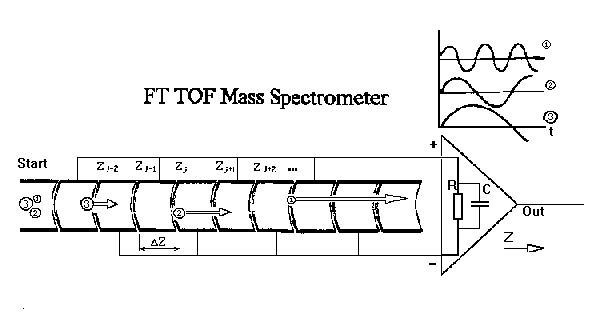 Redistribution of the charge induced by a single moving charge in the periodic array of detecting
electrodes provides information about the ion's velocity.
As the resolution of a Fourier transform is proportional to the number of periods in the
time domain one must provide a reasonably large number of detecting pairs in the array for
resolution to be of practical value. This suggests longer detectors. However, the unfortunate
effect of initial divergences of the incoming beam on the ultimate resolution cannot be eliminated
even by beam focusing using periodic Einzel lens arrays (discussed in [2]
and shown in Fig. below:)
Redistribution of the charge induced by a single moving charge in the periodic array of detecting
electrodes provides information about the ion's velocity.
As the resolution of a Fourier transform is proportional to the number of periods in the
time domain one must provide a reasonably large number of detecting pairs in the array for
resolution to be of practical value. This suggests longer detectors. However, the unfortunate
effect of initial divergences of the incoming beam on the ultimate resolution cannot be eliminated
even by beam focusing using periodic Einzel lens arrays (discussed in [2]
and shown in Fig. below:)
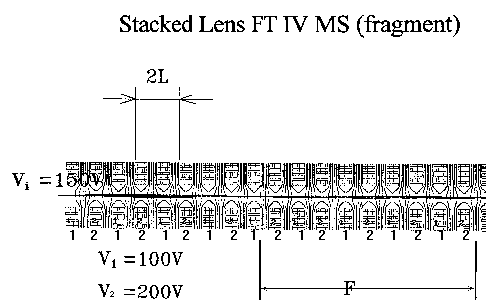 Guiding-detecting electrode groups marked as 1 and 2 are disconnected in a DC sense and
shorted through an operational amplifier in the AC sense using well known
ICR circuitry. The performance of this type of array is
illustrated in Figs below:
Guiding-detecting electrode groups marked as 1 and 2 are disconnected in a DC sense and
shorted through an operational amplifier in the AC sense using well known
ICR circuitry. The performance of this type of array is
illustrated in Figs below:
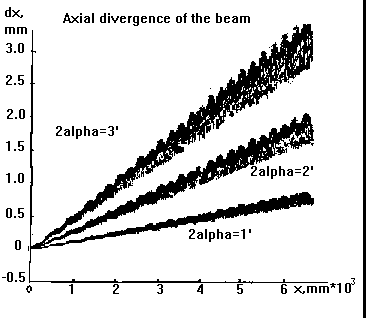
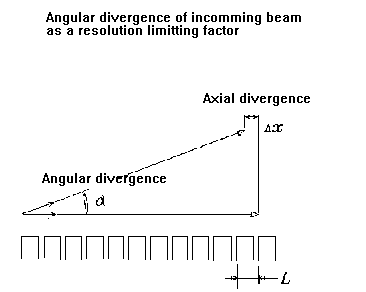 The three diverging modulated curves in the second Fig. reflect
accumulation of the axial divergence, dx (Fig 1 in the later set), by
three ions with different starting angles in a diverging monochromatic
beam. As soon as dx becomes larger then the array cell constant, L, the detected signal is out of
phase (broadened by 2pi) and further detection is senseless.
The three diverging modulated curves in the second Fig. reflect
accumulation of the axial divergence, dx (Fig 1 in the later set), by
three ions with different starting angles in a diverging monochromatic
beam. As soon as dx becomes larger then the array cell constant, L, the detected signal is out of
phase (broadened by 2pi) and further detection is senseless.
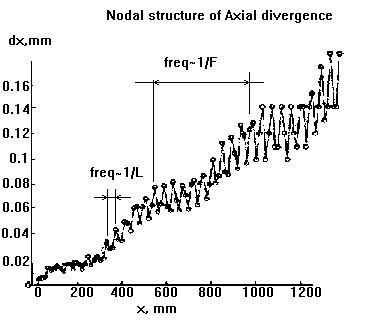
Linearity of the overall axial divergence of the three curves in
Figs above insures that only the
first-order alpha-aberrations are present. Small nodes in the curves correspond to the array cell
constant, L and introduce multiple-harmonics distortion in detected signal. The larger node is
caused by focusing properties of the potential array which depend on geometry and voltages
applied to the lens groups. It introduces only one easily predictable extra harmonic of a much
lower frequency.
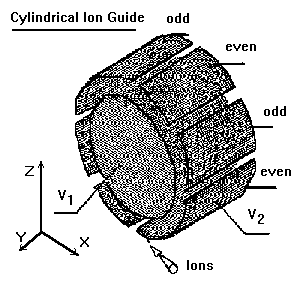
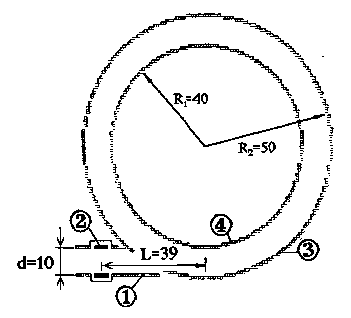
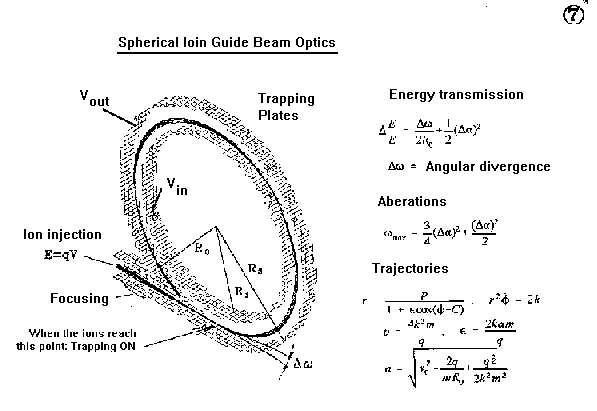
Restricted trajectory ion guides - namely, spherical analyzer ion guide and cylindrical
analyzer ion guide - are shown in Figures below:

![]()
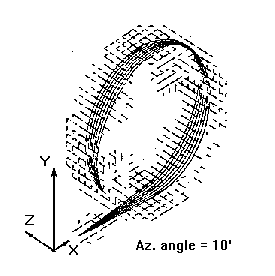 Next set of figures illustrates some aspects of
physics involved in characterization of the
restricted-trajectory guides. Strong advantage of this family of ion guides comes with realizability
of "infinite" ion trajectories, compact size and mechanical simplicity. Analytical studies of
trajectories and resolving power predictions are only slightly more complex and the same major
limitations apply.
Next set of figures illustrates some aspects of
physics involved in characterization of the
restricted-trajectory guides. Strong advantage of this family of ion guides comes with realizability
of "infinite" ion trajectories, compact size and mechanical simplicity. Analytical studies of
trajectories and resolving power predictions are only slightly more complex and the same major
limitations apply.
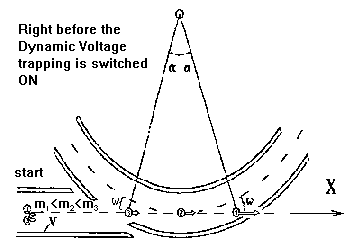
Summary
Simulations of linear geometry array detectors utilizing stacked-lens ion guides have
shown that resolving power of 10^3 is easily achieved for a reasonable scale design (array length
~5m). Simplicity of design, linear relationship between resolving power and tube length, and
simple control of beam divergence can be mentioned as advantages of this class of instruments.
Introducing the added complexity of the HV pulsed-gates to inject
ions into confined -
trajectory ion guides (electrostatic traps or analyzers) removes the limitations of the array size on
the achievable resolving power. Background beam dephasing and storage of the detected signal
become significant considerations. Despite these limitations simulations predict resolution of
10^3-10^4 for desktop size models of the spherical and cylindrical analyzer guides.
Overall FTIV MS appears to be a plausible alternative to B-field based MS and
conceptional TOF MS. Applications may include environmental MS measurements for
instruments of the confined trajectories class, where resolution can be somewhat sacrificed for
compact size, mechanical simplicity and low power requirements. An exotic potential application
(astrophysics) of the linear geometry example is detection of a single charged particle under
conditions of ultra-low background pressure.
Key References
- [1] E.N.Nikolaev, V.S.Rakov and J.H.Futrell, Int.J.Mass Spectrom Ion
Proc, 157/158 (1996)
- 215-232
- [2] P.B.Grosshans, P.J.Shields and A.G.Marshall,J.Chem.Phys, 94(8),
1991
- [3] M.A.May and A.G.Marshall, Anal.Chem. 1992, 64, 1601-1605
- [4] Guan, S.; Marshall, A.G., J. Amer. Soc. Mass Spectrom,1996,
7,101-106
 Redistribution of the charge induced by a single moving charge in the periodic array of detecting
electrodes provides information about the ion's velocity.
As the resolution of a Fourier transform is proportional to the number of periods in the
time domain one must provide a reasonably large number of detecting pairs in the array for
resolution to be of practical value. This suggests longer detectors. However, the unfortunate
effect of initial divergences of the incoming beam on the ultimate resolution cannot be eliminated
even by beam focusing using periodic Einzel lens arrays (discussed in [2]
and shown in Fig. below:)
Redistribution of the charge induced by a single moving charge in the periodic array of detecting
electrodes provides information about the ion's velocity.
As the resolution of a Fourier transform is proportional to the number of periods in the
time domain one must provide a reasonably large number of detecting pairs in the array for
resolution to be of practical value. This suggests longer detectors. However, the unfortunate
effect of initial divergences of the incoming beam on the ultimate resolution cannot be eliminated
even by beam focusing using periodic Einzel lens arrays (discussed in [2]
and shown in Fig. below:)
 Guiding-detecting electrode groups marked as 1 and 2 are disconnected in a DC sense and
shorted through an operational amplifier in the AC sense using well known
ICR circuitry. The performance of this type of array is
illustrated in Figs below:
Guiding-detecting electrode groups marked as 1 and 2 are disconnected in a DC sense and
shorted through an operational amplifier in the AC sense using well known
ICR circuitry. The performance of this type of array is
illustrated in Figs below:


 The three diverging modulated curves in the second Fig. reflect
accumulation of the axial divergence, dx (Fig 1 in the later set), by
three ions with different starting angles in a diverging monochromatic
beam. As soon as dx becomes larger then the array cell constant, L, the detected signal is out of
phase (broadened by 2pi) and further detection is senseless.
The three diverging modulated curves in the second Fig. reflect
accumulation of the axial divergence, dx (Fig 1 in the later set), by
three ions with different starting angles in a diverging monochromatic
beam. As soon as dx becomes larger then the array cell constant, L, the detected signal is out of
phase (broadened by 2pi) and further detection is senseless.


 Next set of figures illustrates some aspects of
physics involved in characterization of the
restricted-trajectory guides. Strong advantage of this family of ion guides comes with realizability
of "infinite" ion trajectories, compact size and mechanical simplicity. Analytical studies of
trajectories and resolving power predictions are only slightly more complex and the same major
limitations apply.
Next set of figures illustrates some aspects of
physics involved in characterization of the
restricted-trajectory guides. Strong advantage of this family of ion guides comes with realizability
of "infinite" ion trajectories, compact size and mechanical simplicity. Analytical studies of
trajectories and resolving power predictions are only slightly more complex and the same major
limitations apply.


