lab08, CISC106, Fall 2007

Special note for Conrad's honors sections only:

On this lab, you may work in pairs.

If you work in pairs,

The words above are specific to this lab.

This does NOT establish a precedent for future labs—unless specifically instructed otherwise, always assume that collaboration at the level of working on code together is not permitted, and may constitute academic dishonesty.

 

Overview

In this lab, we'll cover some basic things about MATLAB, and get more practice with matrices, function M-files, and test scripts.

Step-by-Step Instructions

Step 1: Preliminaries

To prepare for this week's lab, do all the following steps. If you are not sure what to do at any stage, you can consult earlier labs for details:

Step 2: Learning a few things about MATLAB

Each of the steps under this section involves learning something interesting about MATLAB.

(Acknowledgement: The items in Step 2 of this lab (except for step 2e) are adapted from labs written by Dr. Terry Harvey, by permission.)

Step 2a: A surprise

If you type the expression0.3 - 0.2 - 0.1 at the MATLAB prompt, what would you expect the result to be?

Try it and see what result you get. Are you surprised?

Next, use the fprintf() function to examine each of the numbers involved, by changing the width and precision fields of the format specifier so that you can see the numbers with great precision

Once you have learned how to use fprintf to do this, start a diary file called lab08_step2a.txt. In this file, show high precision versions of all the tenths from 0.1 to 1.0. Each should print on a separate line.

To turn in from this step: diary file lab08_step2a.txt

Step 2b: Growing a Matrix

We can change the size of a matrix we are using in Matlab. Start a diary file called lab08_step2b.txt.

Then, show the following sequence of commands:

x = []
x(2) = 9
x(2,2) = 8

What is the size of x after each command? Use the size function to show this (e.g. type size(x))


Being able to “grow” a matrix to fit our needs is a powerful tool, but not without cost—we pay a performance penalty when we grow a Matrix a little bit at a time.

To turn in from this step: diary file lab08_step2b.txt

Step 2c: for loop over the length of a vector


We can use the length() function on a vector to see how long it is, then use the length found to run a for loop that looks at each position in the vector.

For an example, see lengthVector.m in the files you copied for this week's lab.

You can also type help length at the MATLAB prompt to learn more about the length function.

Here's another example of a function M-file that does uses this technique.myMax.m finds the maximum value in a vector. It is in your directory this week, along with a test script called testMyMax.m, and a helper function performEqualTest.m

Note that MATLAB has a built-in function called max() that does this, but that's not the point—finding a maximum is a basic programming skill, so we need to know how to do it even without a built-in function to help us. So, read through this code carefully, because a question about it could show up on a future quiz or exam.

Notice how we initialize theMax to the first value in the vector. We then compare it to every remaining value, and in each case, if that value is bigger, we set theMax to that value instead. In this way, myMax never gets smaller, but it may get larger, and is always guaranteed to be the largest number we've seen so far. (A question to ponder: how would you modify this function M-file to return the minimum instead of the maximum?) 

function theMax = myMax(v)
% myMax   return maximum value in a vector
%
% consumes: v, a vector
% produces: theMax, a scalar, the maximum value in v
%
% Example:
%   >> myMax([3 5 6 2])
%   ans =
%       6
%   >> myMax([])
%   ans = 
%       []
%
% P. Conrad for CISC106, sect 99, 10/22/2007
  
  if (length(v) == 0)
    theMax = [];
  else
    theMax = v(1);
    
    for i=2:length(v)
      
      if (v(i) > theMax)
	     theMax = v(i);
      end; % if
      
    end; % for
  end % if 

    

 return;

  
end % function


Now, for credit: Write a function M-file sevens2pi.m that traverses a vector of any length with a for loop and changes the sevens in the vector to pi. Write a simple test script testSevens2pi.m that shows your function working on both row and column vectors.

Create a diary file lab08_step2c.txt in which you type out the source code of both sevens2pi.m and testSevens2pi.m, and then show that the function passes its tests.

To turn in from this step: diary file lab08_step2c.txt, M-files sevens2pi.m and testSevens2pi.m

Step 2d: for loop over values in a vector

A function that traverses a vector does not always need to calculate the length of a vector. An example file, yetAnotherMax.m is listed below —it is yet another function that returns the maximum value in a vector. The code for that, along with a test script testYetAnotherMax.m is in your directory this week.

Note that the line of code for e = v indicates that e should take on each value of v one at a time. The for loop is repeated for each value of v. (In some programming languages, this is called a foreach loop).

We use e rather than i to indicate that we are processing elements rather than indexes (or indices, if you prefer the more proper form of the plural).

function theMax = yetAnotherMax(v)
% yetAnotherMax   return maximum value in a vector (a different way)
%
% consumes: v, a vector
% produces: theMax, a scalar, the maximum value in v
%
% Example:
%   >> myMax([3 5 6 2])
%   ans =
%       6
%   >> myMax([])
%   ans = 
%       []
%
% P. Conrad for CISC106, sect 99, 10/22/2007
  
  if (isempty(v))
    theMax = [];
  else
    theMax = v(1);
    
    for e=v % e takes on the value of each successive element
      if (e > theMax)
	theMax = e;
      end; % if
      
    end; % for
 end % if 
     
 return;
   
end % function

For credit: Write a function M-file squareVector.m that uses a for loop to compute the square of each member of its vector parameter and store the value in an output vector—but, do not (in any way) find the length of the vector parameter before using it.

Write a simple test script testSquareVector.m that shows your function working on row vectors.

Hint: also review step2b above about growing a matrix. You may need to use an extra variable.

Create a diary file lab08_step2d.txt in which you type out the source code of both squareVector.m and testSquareVector.m, and then show that the function passes its tests.

To turn in from this step: diary file lab08_step2d.txt, M-files squareVector.m and testSquareVector.

Step 2e: fixing the performEqualTest.m script

The performEqualTest.m script has a limitation—it does not behave correctly when passed empty matrices.

It should print "passed" when either

Otherwise it should print "failed".

Change the script so that it works properly.

To test it, you can:

Make a diary file lab08_step2e.txt in which you type out the performEqualTest.m file, and then show that it is working on these two test scripts, with test 4 uncommented.

To turn in:

Step 3: Plotting Line Drawings with MATLAB

There is nothing to turn in from Step 3—it is background for the exercises in Steps 4 and 5, and also for lab09.

Step 3a: Introduction

Suppose we have a set of points that we want to plot that represent a simple drawing---sort of a "connect the dots" style drawing.

For example, suppose we connect:

Then the result is the capital letter A:

http://www.udel.edu/CIS/106/pconrad/wikiExamples/MATLAB/plotting/lineDrawings/letterA.jpg

We can represent a drawing like this using a MATLAB 2xn matrix, as follows:

Furthermore, we can state that if a column is an exact repeat of the previous row, this is a signal that the user should "pick up the pen" and start a new line with the next column.

With these rules in mind, we can represent out letter A as follows: 

>> points = [ 0 0 ; 2 8 ; 4 0 ; 4 0 ; 1 4 ; 3 4 ]'                   

points =

     0     2     4     4     1     3
     0     8     0     0     4     4

>>

Step 3b: Plotting a drawing

How can we plot a drawing represented in this way?

The following MATLAB function M-file can do the job:

plotLineDrawing.m

For example: 

>>  points = [ 0 0 ; 2 8 ; 4 0 ; 4 0 ; 1 4; 3 4 ]';
>>  plotLineDrawing(points,'-djpeg','cisc106/10.18','letterA.jpg') 

ans =

http://copland.udel.edu/~pconrad/cisc106/10.18/letterA.jpg

>>

The resulting plot looks like this:

http://copland.udel.edu/~pconrad/cisc106/10.18/letterA.jpg

Here is another example: a very simple looking tree: 


>> tree = [ 0 4 1; 5 16 1; 10 4 1; 0 4 1; 0 4 1; 4 4 1; 4 0 1; 6 0 1; 6 4 1]'

tree =

     0     5    10     0     0     4     4     6     6
     4    16     4     4     4     4     0     0     4
     1     1     1     1     1     1     1     1     1

>>  plotLineDrawing(tree,'-djpeg','cisc106/10.18','tree.jpg')                   

ans =

http://copland.udel.edu/~pconrad/cisc106/10.18/tree.jpg

>>

And here is what it looks like:

http://copland.udel.edu/~pconrad/cisc106/10.18/tree.jpg

To understand the four parameters, we can use the help that is built into the H1 comment: 

>> help plotLineDrawing
 plotLineDrawing   plot points as a line drawing on the web
 
  consumes: 
    points, a matrix of points to plot 
                    each column is one point (x,y)
                    the first row is all the x values
                    the second row is all the y values
 
                    if there are more then 2 rows, the rest of the
                    rows are ignored; if fewer, an empty matrix is returned
 
                    if a column is repeated, it means pick up the pen
 
    graphicsType: one of the following '-djpeg', '-dpng'
                  (or other legal arg to the function print())
 
    dirName: directory name, relative to ~/public_html
    fileName: a filename in which to store the drawing
 
  produces:
    url: the url at which the graphic can be found, or
         an empty matrix if the graphic cannot be produced.
   
  Example: Plot the capital letter A in the box with 0,0 at lower
           left and 4,8 at upper right.
 
   >> points = [ 0 0 ; 2 8 ; 4 0 ; 4 0 ; 1 4; 3 4 ]';
   >> plotLineDrawing(points,'-djpeg','cisc106/10.18','letterA.jpg') 
   ans = 
 
     http://copland.udel.edu/~pconrad/cisc106/10.18/letterA.jpg
 
   >> 
  P. Conrad   for CISC106, 10/16/2007

>>

Step 3c: Affine transformations

Once we have these points in this fashion, we can apply what are called the Affine Transformations:

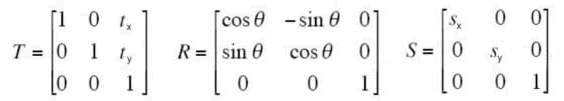
http://www.udel.edu/CIS/106/pconrad/wikiExamples/MATLAB/plotting/lineDrawings/matrix.gif

These are the transformation that translate, rotate, and scale.

To use these transformations, we have to add an extra row of 1's to our points. So instead of: 

>> points = [ 0 0 ; 2 8 ; 4 0 ; 4 0 ; 1 4 ; 3 4 ]'                   

points =

     0     2     4     4     1     3
     0     8     0     0     4     4


>>

We have: 

>> points = [ 0 0 1; 2 8 1; 4 0 1; 4 0 1; 1 4 1; 3 4 1]'                   

points =

     0     2     4     4     1     3
     0     8     0     0     4     4
     1     1     1     1     1     1
>>

Fortunately, our plotting routine doesn't care if this extra row is there---it just ignores it.

Why this extra row of ones? The short answer is: it makes the math work out. For a more satisfying answer, take a linear algebra course, a computer graphics or do some research on the web or at the library. For our purposes, we'll take this as given.

With this extra row in place, we can do scaling very easily. For example, if we want to scale the letter A by a factor of 3 in the x direction, and a factor of 4 in the y direction, we can type this: 

>>  points = [ 0 0 1; 2 8 1; 4 0 1; 4 0 1; 1 4 1; 3 4 1]'          

points =

     0     2     4     4     1     3
     0     8     0     0     4     4
     1     1     1     1     1     1

>> s = scaleIt(3,4)

s =

     3     0     0
     0     4     0
     0     0     1

>> newPoints = s * points 

newPoints =

     0     6    12    12     3     9
     0    32     0     0    16    16
     1     1     1     1     1     1

>>  plotLineDrawing(newPoints,'-djpeg','cisc106/10.18','scaledA.jpg') 

ans =

http://copland.udel.edu/~pconrad/cisc106/10.18/scaledA.jpg

>>

And the resulting plot looks like this:

http://copland.udel.edu/~pconrad/cisc106/10.18/scaledA.jpg

The .m file for the scaleIt() function, scaleIt.m is very simple--with the exception of the H1 comment, it is really little more than one line of code: 

function result = scaleIt(sx,sy)
% scaleIt   return matrix for scaling of 2D graphics

...

  result = [ sx 0 0; 0 sy 0; 0 0 1];
  return;
end

Here's a link to the complete code: scaleIt.m

Step 4: Write the functions for translating and rotating

Using the scaleIt.m function M-file given above as an example, and the affine formulas given earlier on this web page for translation and rotation, write similar function M-files to produce functions like these:

(a) a function to do translation 

function result = translateIt(tx,ty)
%rotateIt   matrix for 2D translation by tx and ty

(b) a function to do rotation 

function result = rotateIt(phi)
%rotateIt   matrix for 2D rotation around origin by phi radians

(c) as a convenience, a function that rotates in degrees instead of radians:
(hint: use a call to the radians version inside your function body). 

function result = rotateItDeg(phi)
%rotateIt   matrix for 2D rotation around origin by phi degrees

In each case, write the function M-file, and a test script.

Then:

Finally

To turn in:

On the web

Step 5: Fixing the axes

Some figures---for example, a square---don't look too good with the axis equal tight command that is inside plotLineDrawing.m. For example, while we can plot the letter A just fine, if we plot the letter L, we'll see nothing, because the lines are coincident with the x and y axes.

Similar, if we plot a square, all four edges will be obscured by the edges of the plot.

To fix this, you can write a function findLimits like this: 

function [xmin xmax ymin ymax] = findLimits(points)
%findLimits  find x,y limits in a set of points for a line drawing
%
% consumes: points, a matrix of points (in format expected by plotLineDrawing.m)
%           see "help plotLineDrawing" for more details
%
% produces: xmin, xmax: the minimum and maximum values from points(1,:),
%                        i.e. the x coordinates of all the points in the drawing
%           ymin, ymax: the minimum and maximum values from points (2,:),
%                        i.e. the y coordinates of all the points in the drawing
...

Then, make a new version of plotLineDrawing.m that uses this function like this: 

   [xmin xmax ymin ymax] = findLimits(points);
   axis ([xmin-1  xmax+1  ymin-1  ymax+1]);

Another option is to write the function as: 

function limits = findLimits(points)

and have the function return a vector containing the four elements. In that case, you'll have to do a bit more work inside the plotLineDrawing() function to adjust the four values before passing them to the built-in axis function of MATLAB.

You should also figure out how you can also specify that you want the "equal" option on the axis command so that the aspect ratio is preserved---that is, the x and y units are the same size on the plot that is produced.

What you need to do for credit

To do this properly

Here are a few. test cases to help you in your thinking. Let's suppose that you are using this as your prototype (though it is your choice whether to use this, or the [xmin xmax ymin ymax] version) 

function limits = findLimits(points)

If the input is the A matrix shown below: 

>> A                

A =

     0     2     4     4     1     3
     0     8     0     0     4     4
     1     1     1     1     1     1

>> actual = findLimits(A)
...

then the expected value would be [0 4 0 8].

But if the input were the house matrix: 

>> load house.dat
>> house

house =

    40   120   120    40    40    40    40    80   120   120    72    72    88    88
    80    80   170   170    80    80   170   200   170   170    80   125   125    80
     1     1     1     1     1     1     1     1     1     1     1     1     1     1

>> actual = findLimits(house)
...

In this case, expected should be [40 120 80 200]

If you have any questions about exactly what you are supposed to do, ask your instructor or your TA.

Um, I'm stuck---I know what I'm supposed to do, but I don't know how

Ok, so it turns out that MATLAB already has a function built in function called min that will help you find the smallest element in a Matrix. However, it requires you to read the documentation, which can be found here:

http://www.mathworks.com/access/helpdesk/help/techdoc/index.html?/access/helpdesk/help/techdoc/ref/min.html

You have to figure out exactly how to get at what we want, which is:

Some questions to guide you:

Some additional suggestions:

Step 6: Make a zip file lab08.zip of your files

As with last week, we are going to create a zip file. This time we are just going to take all .m, .txt and .dat files inside your lab08 directory. The diary files will be included inside your zip file, so that's the only file you'll have to submit on WebCT.

To create and test the zip file, follow the instructions from step11 of lab06 and/or lab07.

Step 7: Submit your lab08.zip file

Now you can submit your work on WebCT, and you are done!

Grading: 100 Points

 

step what we're looking for points
step 2a
  • lab08_step2a.txt
    10 pts for following directions
    (i.e. showing value of 0.1, 0.2, etc. at high precision)
10
step 2b
  • lab08_step2b.txt
    10 pts for following directions
    (i.e. showing size of matrix after each step)
10
step 2c
  • sevens2pi.m (5 pts for correctness, 5 for style)
  • testSevens2pi.m (5 pts for correctness, 5 for style)
  • lab08_step2c.txt (10 pts)
 30
step 2d
  • squareVector.m (5 pts for correctness, 5 for style)
  • testSquareVector.m (5 pts for correctness, 5 for style)
  • lab08_step2d.txt(10 pts)
30
step 2e
  • performEqualTest.m (5 pts for correctness of changed file, 5 for style)
  • lab08_step3e.txt (10 pts)
20
step 4 110
step 5
  • testFindLimits.m (5 pts for correctness of changed file, 5 for style)
  • findLimits.m (5 pts for correctness of changed file, 5 for style)
  • function call to findLimits() in plotLineDrawing.m (5 pts)
  • fixing the aspect ratio with correct use of equal option of axis built-in function (5 pts)
  • re-running initPlot.m, as reflected in the fact that plots on the web from step 4 have the extra space around them. (20 pts, 5 pts each)
  • No diary is necessary for this step.
50
step 6
  • Correctly creating the lab08.zip file
20
step 7
  • Submitting only lab08.zip on WebCT
10
overall following of directions student should follow any and all other directions given 10
Total    

 

End of lab08 for CISC106, Fall 2007
Due Date: Nov 1, 2007  Extended to Tuesday Nov 6, 2007, 11:55pm